题目内容
若三角形两边a、b满足3a2-ab-24b2=0,则
的值为( )
| a |
| b |
分析:推出3a+8b)(a-3b)=0,得出3a+8b=0,a-3b=0,求出a=-
b,a=3b,根据三角形的边长不能为负数,只取a=3b,代入求出即可.
| 8 |
| 3 |
解答:解:3a2-ab-24b2=0,
(3a+8b)(a-3b)=0,
∴3a+8b=0,a-3b=0,
∴a=-
b,a=3b,
∵a、b表示三角形的两边,
∴a=-
b舍去,
当a=3b时,
=
=3,
故选A.
(3a+8b)(a-3b)=0,
∴3a+8b=0,a-3b=0,
∴a=-
| 8 |
| 3 |
∵a、b表示三角形的两边,
∴a=-
| 8 |
| 3 |
当a=3b时,
| a |
| b |
| 3b |
| b |
故选A.
点评:本题考查了解一元二次方程的应用,关键是求出a=3b,题目较好,有一定的难度.

练习册系列答案
相关题目
 的值为
的值为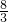
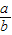 的值为( )
的值为( )
 或3
或3 或-3
或-3