题目内容
【题目】如图，已知AB∥CD,∠EAF =
∠EAB,∠ECF=∠ECD ,∠AFC=62°,则∠AEC度数是________
【答案】93°
【解析】
连接AC，设∠EAF=x°，∠ECF=y°，则∠EAB=3x°，∠ECD=3y°，可得∠BAF=2x°，∠DCF=2y°，由AB∥CD，三角形的内角和定理，可得∠AFC=2（x°+y°）=62°，计算得到x°+y°=31°，则∠AEC=3（x°+y°），即可得到答案.
解，如图，连接AC，设∠EAF=x°，∠ECF=y°，
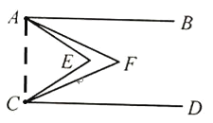
∴∠EAB=3x°，∠ECD=3y°，
∴∠BAF=2x°，∠DCF=2y°，
∵AB∥CD，
∴∠BAC+∠ACD=180°，
∴∠BAF+∠FAC+∠ACF+∠DCF=180°，
∵∠FAC+∠ACF+∠AFC=180°，
∴∠AFC=∠BAF+∠DCF=2（x°+y°）=62°，
∴x°+y°=31°.
同理可求：∠AEC=∠BCE+∠DCE=3（x°+y°），
∴∠AEC=
.
故答案为：93°.
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
