题目内容
如图，等边三角形ABC，点E是AB上一点，点D在CB的延长线上，且ED=EC，
EF∥AC交BC于点F．
(1)试说明四边形AEFC是等腰梯形；
(2)请判断AE与DB的数量关系，并说明你的理由．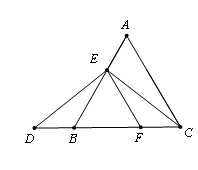
EF∥AC交BC于点F．
(1)试说明四边形AEFC是等腰梯形；
(2)请判断AE与DB的数量关系，并说明你的理由．
(1)四边形AEFC是等腰梯形 (3′)
(2) AE＝DB (8′)
(2) AE＝DB (8′)
本题考查了等腰梯形的判定，全等三角形的性质和判定，等边三角形的性质的应用. （1）根据平行得出梯形AEFC，根据等边三角形性质得出∠A=∠ACB，根据等腰梯形的判定推出即可；（2）求出AE=CF，推出∠EFB=∠ACB=∠ABC，推出∠D=∠ECD，根据AAS证出△EFD≌△EBC，得出DF=BC，推出BD=CF即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
