Question

【题目】已知，如图，双曲线y= （x＞0）与直线EF交于点A，点B，且AE=AB=BF，连结AO，BO，它们分别与双曲线y= （x＞0）交于点C，点D，则：

（1）①AB与CD的位置关系是；
②四边形ABDC的面积为 ．

Answer 1

【答案】
（1）AB∥CD；
【解析】解：①如图，过点A作AM⊥x轴于点M，过点D作DH⊥x轴于点H，过点B作BN⊥x轴于点N，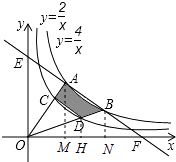

∴AM∥DH∥BN∥y轴，
设点A的坐标为：（m， ），
∵AE=AB=BF，
∴OM=MN=NF，
∴点B的坐标为：（2m， ），
∴S△OAB=S△OAM+S梯形AMNB﹣S△OBN=2+ ×（ + ）×（2m﹣m）﹣2=3，
∵DH∥BN，
∴△ODH∽△OBN，
∴ ，
∵DHOH=2，BNON=4，
∴（ ）2= = ，
同理：（ ）2= ，
∴ = ，
∴AB∥CD
所以答案是：AB∥CD
②∵ = ，∠COD=∠AOB，
∴△COD∽△AOB，
∴ =（ ）2= ，
∴S△COD= ，
∴S四边形ABDC= ．
所以答案是： ．