题目内容
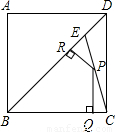
（2003•河北）如图：MN为⊙O的切线，A为切点，过点A作AP⊥MN交⊙O的弦BC于点P，若PA=2cm，PB=5cm，PC=3cm．则⊙O的直径为9.5
9.5
cm．分析：作辅助线，延长AP交⊙O于点D，由AP⊥MN，可知AP过圆心O，由相交弦定理可知，PA•PD=PB•PC，将数据代入，可将PD的长求出，故⊙O的直径AD=AP+PD．
解答：
解：延长AP交⊙O于点D，
∵PA•PD=PC•PB，
∴2×PD=3×5，
∴PD=7.5cm，
∴⊙O的直径AD=PA+PD=2+7.5=9.5cm．
解：延长AP交⊙O于点D，∵PA•PD=PC•PB，
∴2×PD=3×5，
∴PD=7.5cm，
∴⊙O的直径AD=PA+PD=2+7.5=9.5cm．
点评：本题主要考查切线的性质及相交弦定理的应用．
练习册系列答案
相关题目
