题目内容
 已知等腰△ABC中,AB=AC,
已知等腰△ABC中,AB=AC,(1)若cos∠B=
| 1 |
| 3 |
(2)若tan∠A=
| ||
| 2 |
| 3 |
分析:(1)过点A作AD⊥BC,垂足为D,根据余弦的定义即可求解;
(2)作BH⊥AC于点H,∴∠AHB=90°,根据直角三角形的性质即可求解.
(2)作BH⊥AC于点H,∴∠AHB=90°,根据直角三角形的性质即可求解.
解答:解:(1)过点A作AD⊥BC,垂足为D,
∴∠ADB=90°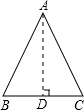
∴在△ADC中,cos∠B=
=
,
设BD=k,AB=3k.
∵AB=AC,AD⊥BC
∴BD=DC=k,
∵△ABC的周长为24,
∴AB+AC+BC=24.
∴3k+3k+2k=24,即8k=24,
∴k=3
∴AB=9;
(2)解:作BH⊥AC于点H,
∴∠AHB=90°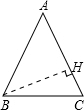
∴在△AHB中,tan∠A=
=
,
设BH=
k,AH=2k.
在Rt△ABH中,AB=
=3k.
∵AB=AC,
∴CH=AC-HC=k,
∵在△BHC中,BH=
k,CH=k,BC=2
,
又∵∠BHC=90°.
∴BH2+HC2=BC2,即5x2+x2=12
解得:x=
,
∴AB=3
.
∴∠ADB=90°

∴在△ADC中,cos∠B=
| BD |
| AB |
| 1 |
| 3 |
设BD=k,AB=3k.
∵AB=AC,AD⊥BC
∴BD=DC=k,
∵△ABC的周长为24,
∴AB+AC+BC=24.
∴3k+3k+2k=24,即8k=24,
∴k=3
∴AB=9;
(2)解:作BH⊥AC于点H,
∴∠AHB=90°

∴在△AHB中,tan∠A=
| BH |
| AH |
| ||
| 2 |
设BH=
| 5 |
在Rt△ABH中,AB=
| AH2+BH2 |
∵AB=AC,
∴CH=AC-HC=k,
∵在△BHC中,BH=
| 5 |
| 3 |
又∵∠BHC=90°.
∴BH2+HC2=BC2,即5x2+x2=12
解得:x=
| 2 |
∴AB=3
| 2 |
点评:本题考查了解直角三角形,属于基础题,关键是掌握直角三角形的基本性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度; 12、如图:已知等腰△ABC中,腰AB=AC=13cm,底BC=24cm,求△ABC的面积.
12、如图:已知等腰△ABC中,腰AB=AC=13cm,底BC=24cm,求△ABC的面积.