题目内容
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的
平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
=;min{-1,2,3}=-1;min{-1,2,a}=
解决下列问题:
(1)min
{,,}
若min{2,2x+2,4-2x}=2,则x的范围为
;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么
(填a,b,c的大小关系)”.证明你发现的结论;
③运用②的结论,填空:
若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=
.
分析:①M{a,b,c}表示这a,b,c三个数的平均数,即求
的值;
②min{a,b,c}表示这a,b,c三个数中最小的数,即比较三个数的大小哪一个最小.
解答:解:(1)min
{,,}=
;
由min{2,2x+2,4-2x}=2,得
,即0≤x≤1.
(2)①∵M{2,x+1,2x}=min{2,x+1,2x},∴
,即
,∴x=1
②证明:由M{a,b,c}=min{a,b,c},可令
=a,即b+c=2a⑤;
又∵
,解之
得:a+c≤2b ⑥,a+b≤2c⑦;
由⑤⑥可得c≤b;由⑤⑦可得b≤c;
∴b=c;将b=c代入⑤得c=a;
∴a=b=c.
③据②可得
,
解之得y=-1,x=-3,
∴x+y=-4.
点评:本题解决的关键是读懂题意,据题意结合方程和不等式去求解,考查综合应用能力.
练习册系列答案
相关题目

 名校课堂系列答案
名校课堂系列答案 阅读以下材料:
阅读以下材料: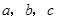 ,用
,用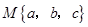 表示这三个数的平均数,用
表示这三个数的平均数,用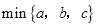 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: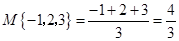 ;
;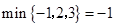 ;
;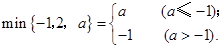
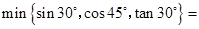 ;
;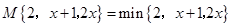 ,求
,求 ;
;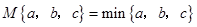 ,那么 (填
,那么 (填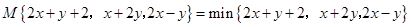 ,则
,则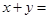 .
.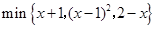 的最大值为 .
的最大值为 . ,用
,用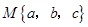 表示这三个数的平均数,用
表示这三个数的平均数,用 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: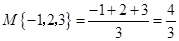 ;
;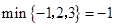 ;
;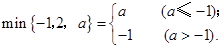
 ;
;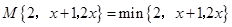 ,求
,求 ;
;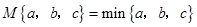 ,那么 (填
,那么 (填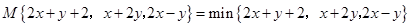 ,则
,则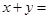 .
.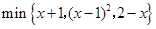 的最大值为 .
的最大值为 .