题目内容
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:
M{-1,2,3}=
| -1+2+3 |
| 3 |
| 4 |
| 3 |
|
解决下列问题:
(1)填空:
如果min{2,2x+2,4-2x}=2,则x的取值范围为
(2)如果M{2,x+1,2x}=min{2,x+1,2x},求x.
分析:根据题中的运算规则得到不等式求解即可.
解答:解:(1)由题意得:
,
求解得:0≤x≤1.
(2)M{2,x+1,2x}=
=x+1.
法一:∵2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,∴x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,∴x=1(舍去).
综上所述:x=1.
法二:∵M{2,x+1,2x}=
=x+1=min{2,x+1,2x},
∴
,
∴
,
∴x=1.
|
求解得:0≤x≤1.
(2)M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
法一:∵2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,∴x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,∴x=1(舍去).
综上所述:x=1.
法二:∵M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
∴
|
∴
|
∴x=1.
点评:解决问题的关键是读懂题意,依题意列出不等式进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 阅读以下材料:
阅读以下材料: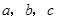 ,用
,用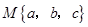 表示这三个数的平均数,用
表示这三个数的平均数,用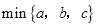 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: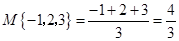 ;
;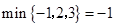 ;
;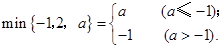
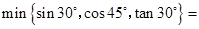 ;
;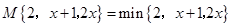 ,求
,求 ;
;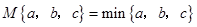 ,那么 (填
,那么 (填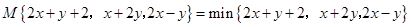 ,则
,则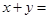 .
.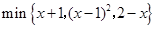 的最大值为 .
的最大值为 . ,用
,用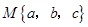 表示这三个数的平均数,用
表示这三个数的平均数,用 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: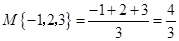 ;
;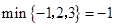 ;
;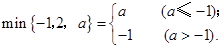
 ;
;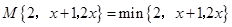 ,求
,求 ;
;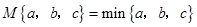 ,那么 (填
,那么 (填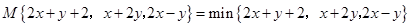 ,则
,则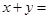 .
.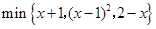 的最大值为 .
的最大值为 .