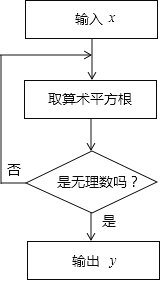
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣ¬δ ΒΫΧ”ΐΨ÷ΓΑΫΧ”ΐ–≈œΔΜ·2.0––Ε·ΦΤΜ°Γ±Θ§¥νΫ® ΐΉ÷Μ·–Θ‘ΑΤΫΧ®Θ§–η“ΣΙΚ¬ρ“Μ≈ζΒγΉ”ΑΉΑεΚΆΤΫΑεΒγΡ‘Θ§»τΙΚ¬ρ2Χ®ΒγΉ”ΑΉΑεΚΆ6Χ®ΤΫΑεΒγΡ‘Ι≤–η9Άρ‘ΣΘΜΙΚ¬ρ3Χ®ΒγΉ”ΑΉΑεΚΆ4Χ®ΤΫΑεΒγΡ‘Ι≤–η11Άρ‘ΣΘ°
Θ®1Θ©«σΒγΉ”ΑΉΑεΚΆΤΫΑεΒγΡ‘ΒΡΒΞΦέΗς «Εύ…ΌΆρ‘ΣΘΩ
Θ®2Θ©ΫαΚœ―ß–Θ ΒΦ Θ§ΗΟ–ΘΉΦ±ΗΙΚ¬ρΒγΉ”ΑΉΑεΚΆΤΫΑεΒγΡ‘Ι≤100Χ®Θ§Τδ÷–ΒγΉ”ΑΉΑε÷Ν…ΌΙΚ¬ρ6Χ®«“≤Μ≥§Ιΐ24Χ®Θ§Ρ≥…ΧΦ“Ηχ≥ωΝΥΝΫ÷÷”≈ΜίΖΫΑΗΘ§ΖΫΑΗ“ΜΘΚΒγΉ”ΑΉΑεΚΆΤΫΑεΒγΡ‘Ψυ¥ρΨ≈’έΘΜΖΫΑΗΕΰΘΚ¬ρ1Χ®ΒγΉ”ΑΉΑεΘ§ΥΆ1Χ®ΤΫΑεΒγΡ‘Θ°»τΙΚ¬ρΒγΉ”ΑΉΑεaΘ®Χ®Θ©Υυ–ηΒΡΖ―”ΟΈΣWΘ®Άρ‘ΣΘ©Θ§«κΗυΨίΝΫ÷÷”≈ΜίΖΫΑΗΖ÷±π–¥≥ωWΙΊ”ΎaΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΖ÷ΈωΗΟ–Θ”Π―Γ”ΟΡΡ÷÷”≈ΜίΖΫΑΗΙΚ¬ρΗϋ Γ«°Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΒγΉ”ΑΉΑεΒΡΒΞΦέ «3Άρ‘ΣΘ§ΤΫΑεΒγΡ‘ΒΡΒΞΦέ «0.5Άρ‘ΣΘΜΓΛΘ®2Θ©ΖΫΑΗ“ΜΘΚWΙΊ”ΎaΒΡΚ· ΐΙΊœΒ Ϋ «WΘΫ2.25a+45Θ§ΖΫΑΗΕΰΘΚWΙΊ”ΎaΒΡΚ· ΐΙΊœΒ Ϋ «WΘΫ2a+50Θ§Β±6ΓήaΘΦ20 ±Θ§ΖΫΑΗ“ΜΗϋ Γ«°Θ§Β±aΘΫ20 ±Θ§ΝΫ÷÷ΖΫΑΗΜ®Ζ―“Μ―υΘ§Β±20ΘΦxΓή24 ±Θ§ΖΫΑΗΕΰΗϋ Γ«°Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΘ§Ν–≥ωœύ”ΠΒΡΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΘ§¥”ΕχΩ…“‘«σΒΟΒγΉ”ΑΉΑεΚΆΤΫΑεΒγΡ‘ΒΡΒΞΦέΗς «Εύ…ΌΆρ‘ΣΘΜ
Θ®2Θ©ΗυΨίΧβ“βΘ§Ζ÷±π–¥≥ωΝΫ÷÷ΖΫΑΗœ¬Θ§WΙΊ”ΎaΒΡΚ· ΐΙΊœΒ ΫΘ§‘Όάϊ”ΟΖ÷άύΧ÷¬έΒΡΖΫΖ®Ω…“‘ΒΟΒΫΗΟ–Θ”Π―Γ”ΟΡΡ÷÷”≈ΜίΖΫΑΗΙΚ¬ρΗϋ Γ«°Θ°
ΫβΘΚΘ®1Θ©…ηΙΚ¬ρΒγΉ”ΑΉΑεΒΡΒΞΦέΈΣxΆρ‘ΣΘ§ΤΫΑεΒγΡ‘ΒΡΒΞΦέ «yΆρ‘ΣΘ§
![]() Θ§
Θ§
ΫβΒΟΘΚ ![]() Θ§
Θ§
¥πΘΚΒγΉ”ΑΉΑεΒΡΒΞΦέ «3Άρ‘ΣΘ§ΤΫΑεΒγΡ‘ΒΡΒΞΦέ «0.5Άρ‘ΣΘΜΓΛ
Θ®2Θ©”…Χβ“βΩ…ΒΟΘ§
ΖΫΑΗ“ΜΘΚWΘΫ[3a+0.5Θ®100©¹aΘ©]ΓΝ0.9ΘΫ2.25a+45Θ§
ΖΫΑΗΕΰΘΚWΘΫ3a+0.5Θ®100©¹a©¹aΘ©ΘΫ2a+50Θ§
Β±2.25a+45ΘΦ2a+50 ±Θ§ΒΟaΘΦ20Θ§
Φ¥Β±6ΓήaΘΦ20 ±Θ§―Γ‘ώΖΫΑΗ“ΜΘΜ
Β±2.25a+45ΘΫ2a+50 ±Θ§ΒΟaΘΫ20Θ§
Φ¥Β±aΘΫ20 ±Θ§ΖΫΑΗ“ΜΚΆΖΫΑΗΕΰΜ®Ζ―“Μ―υΕύΘΜ
Β±2.25a+45ΘΨ2a+50Θ§ΒΟaΘΨ20Θ§
Φ¥Β±20ΘΦxΓή24 ±Θ§―Γ‘ώΖΫΑΗΕΰΘΜ
¥πΘΚΖΫΑΗ“ΜΘΚWΙΊ”ΎaΒΡΚ· ΐΙΊœΒ Ϋ «WΘΫ2.25a+45Θ§ΖΫΑΗΕΰΘΚWΙΊ”ΎaΒΡΚ· ΐΙΊœΒ Ϋ «WΘΫ2a+50Θ§Β±6ΓήaΘΦ20 ±Θ§ΖΫΑΗ“ΜΗϋ Γ«°Θ§Β±aΘΫ20 ±Θ§ΝΫ÷÷ΖΫΑΗΜ®Ζ―“Μ―υΘ§Β±20ΘΦxΓή24 ±Θ§ΖΫΑΗΕΰΗϋ Γ«°Θ°

 ≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ
≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ