题目内容
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.

![]() 求这条直线的函数关系式及点
求这条直线的函数关系式及点![]() 的坐标.
的坐标.
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
![]() 过线段
过线段![]() 上一点
上一点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限,点
在第一象限,点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?
【答案】(1) 直线![]() ,B(8,16);(2)存在,
,B(8,16);(2)存在,![]() 或
或![]() ,理由见解析;(3)当
,理由见解析;(3)当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]()
【解析】
(1)首先求得点A的坐标,然后利用待定系数法确定直线的解析式,从而求得直线与抛物线的交点坐标;
(2)如图1,过点B作BG∥x轴,过点A作AG∥y轴,交点为G,然后分若∠BAC=90°,则AB2+AC2=BC2;若∠ACB=90°,则AB2=AC2+BC2;若∠ABC=90°,则AB2+BC2=AC2三种情况求得m的值,从而确定点C的坐标;
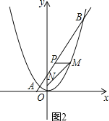
(3)设M(a,![]() a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=
a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=![]() a2+1,然后根据点P与点M纵坐标相同得到x=
a2+1,然后根据点P与点M纵坐标相同得到x=![]() ,从而得到MN+3PM=-
,从而得到MN+3PM=-![]() a2+3a+9,确定二次函数的最值即可.
a2+3a+9,确定二次函数的最值即可.
解:![]() ∵点
∵点![]() 是直线与抛物线的交点,且横坐标为
是直线与抛物线的交点,且横坐标为![]() ,
,
∴![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
设直线的函数关系式为![]() ,
,
将![]() ,
,![]() 代入得
代入得![]() ,
,
解得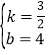 ,
,
∴直线![]() ,
,
∵直线与抛物线相交,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
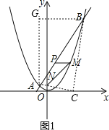
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,交点为
轴,交点为![]() ,
,
∴![]() ,
,
∵由![]() ,
,![]() 可求得
可求得![]() .
.
设点![]() ,同理可得
,同理可得![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
②若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;
;
③若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,![]() 设
设![]() ,如图
,如图![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵点![]() 与点
与点![]() 纵坐标相同,
纵坐标相同,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() ,
,
又∵![]() ,
,
∴取到最小值![]() ,
,
∴当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]() .
.

练习册系列答案
相关题目





