题目内容
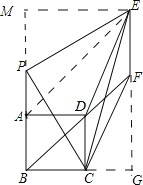
【题目】已知正方形![]() ,点
,点![]() 为射线
为射线![]() 上的一点(不和点
上的一点(不和点![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() ,且
,且![]() ,过
,过![]() 作
作![]() 交射线
交射线![]() 于
于![]() .若
.若![]() 的面积与四边形
的面积与四边形![]() 的面积之比为
的面积之比为![]() ,则
,则![]() ________.
________.

【答案】![]() 或
或![]() .
.
【解析】
作EM⊥BA的延长线于点M,延长EF交BC的延长线于点G,易证△PEM≌△PBC,四边形CDEF为平行四边形,则ME=BP=FG=AB+AP,AP=CG.设AB=BC=1,AP=CG=x,用含x的代数式分别表示S△EFC,S四边形PEFC,根据△EFC与四边形PEFC的面积之比为 3:20,列出关于x的方程,解方程求出x的值,然后根据正切函数的定义即可求出tan∠BPC的值.
作EM⊥BA的延长线于点M,延长EF交BC的延长线于点G,
∵PE⊥PC,
∴∠MPE+∠BPC=90°,
∵∠MPE+∠MEP=90°,
∴∠MEP=∠BPC,
在Rt△PBC和Rt△EMP中
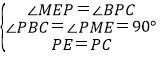
∴Rt△PBC≌Rt△EMP(AAS)
∴PM=BC,ME=PB;
∴PM=AB,
∴PM+PA=AB+PA,
∴MA=ME,
∵MA=ME,AM⊥EM,
∴∠MAE=45°,
∴PB∥EF,
∴四边形ABFE是平行四边形,
∴AB=EF,
∴CD=EF,
∴四边形EFCD是平行四边形,
∴ME=BP=FG=AB+AP,AP=CG,
设AB=BC=1,AP=CG=x,则
S四边形PEFC=S矩形BMEG﹣2S三角形BPC﹣S三角形FCG=(2+x)(1+x)﹣(1+x)﹣![]() (1+x)x=
(1+x)x=![]() x2+
x2+![]() x+1,
x+1,
S△EFC=![]() x;
x;
∵△EFC与四边形PEFC的面积之比为![]() ,
,
∴![]() x:(
x:(![]() x2+
x2+![]() x+1)=3:20,
x+1)=3:20,
解得x=3或![]() ,
,
∵tan∠BPC=![]() ,
,
∴当x=3时,tan∠BPC=![]() ;
;
当x=![]() 时,tan∠BPC=
时,tan∠BPC=![]() .
.
tan∠BPC=![]() 或
或![]() .
.
故答案是:![]() 或
或![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目







