题目内容
【题目】如图,点P是AOB内任意一点,OP=10cm,点P与点![]() 关于射线OA对称,点P与点
关于射线OA对称,点P与点![]() 关于射线OB对称,连接
关于射线OB对称,连接![]() 交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。
交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。

【答案】30°
【解析】
连接OP1,OP2,据轴对称的性质得出∠P1OA=∠AOP=![]() ∠P1OP,∠P2OB=∠POB=
∠P1OP,∠P2OB=∠POB=![]() POP2,PC=CP1,OP=OP1=10cm,DP2=PD,OP=OP2=10cm,求出△P1OP2是等边三角形,即可得出答案.
POP2,PC=CP1,OP=OP1=10cm,DP2=PD,OP=OP2=10cm,求出△P1OP2是等边三角形,即可得出答案.
解:如图:连接OP1,OP2,
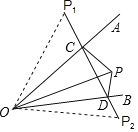
∵点P关于射线OA对称点为点P1
∴OA为PP1的垂直平分线
∴∠P1OA=∠AOP=![]() ∠P1OP,
∠P1OP,
∴PC=CP1,OP=OP1=10cm,
同理可得:∠P2OB=∠POB=![]() ∠POP2,DP2=PD,OP=OP2=10cm,
∠POP2,DP2=PD,OP=OP2=10cm,
∴△PCD的周长是=CD+PC+PD=CD+CP1+DP2=P1 P2=10cm
∴△P1OP2是等边三角形,
∴∠P1OP2=60°,
∴∠AOB=30°,
故答案为:30°

练习册系列答案
相关题目







