��Ŀ����
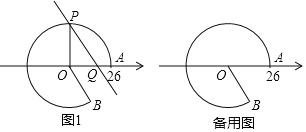
����Ŀ����ͼ����A�������϶�Ӧ����Ϊ26����ԭ��OΪԲ�ģ�OAΪ�뾶���Ż�![]() ��ʹ��B��O���·�����tan��AOB=
��ʹ��B��O���·�����tan��AOB=![]() �����Ż�
�����Ż�![]() ����ȡһ��P�����ܹ�P��ֱ��l��OB�������ڵ�Q����Q�������϶�Ӧ����Ϊx������OP��
����ȡһ��P�����ܹ�P��ֱ��l��OB�������ڵ�Q����Q�������϶�Ӧ����Ϊx������OP��
��1�����Ż���һ��![]() �ij�Ϊ13�������AOP�Ķ�����x��ֵ��
�ij�Ϊ13�������AOP�Ķ�����x��ֵ��
��2����x����Сֵ����ָ����ʱֱ��l��![]() ����Բ��λ�ù�ϵ��
����Բ��λ�ù�ϵ��
��3�����߶�PQ�ij�Ϊ12.5��ֱ��д����ʱx��ֵ��
���𰸡���1����POA=90�㣬x=![]() ����2����ֱ��PQ���O����ʱʱ����ʱx��ֵΪ��32.5����3������������x��ֵΪ��16.5��31.5��31.5��
����2����ֱ��PQ���O����ʱʱ����ʱx��ֵΪ��32.5����3������������x��ֵΪ��16.5��31.5��31.5��
����������1�����û�����ʽ���Բ�ĽǼ��ɽ�����⣻
��2����ͼ��ֱ��PQ���O����ʱʱ��x��ֵ��С��
��3������P���Ż�![]() �ϵ�����һ�㣬����P���λ�÷��������Σ��ֱ���⼴�ɽ�����⣮
�ϵ�����һ�㣬����P���λ�÷��������Σ��ֱ���⼴�ɽ�����⣮
��1����ͼ1�У�
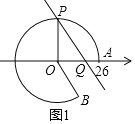
��![]() =13��
=13�У�
���n=90�㣬
���POQ=90�㣬
��PQ��OB��
���PQO=��BOQ��
��tan��PQO=tan��QOB=![]() ��
��
��OQ=![]() ��
��
��x=![]() ��
��
��2����ͼ��ֱ��PQ���O����ʱʱ��x��ֵ��С��

��Rt��OPQ��OQ=OP��![]() =32.5��
=32.5��
��ʱx��ֵΪ��32.5��
��3�������������
����ͼ2�У���OH��PQ��H����OH=4k��QH=3k��

��Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5��3k��2��
�����ã�k2��3k��20.79=0��
���k=6.3��3.3����������
��OQ=5k=31.5��
��ʱx��ֵΪ31.5��
����ͼ3�У���OH��PQ��PQ���ӳ�����H����OH=4k��QH=3k��

��Rt����Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5+3k��2��
�����ã�k2+3k��20.79=0��
���k=��6.3����������3.3��
��OQ=5k=16.5��
��ʱx��ֵΪ��16.5��
����ͼ4�У���OH��PQ��H����OH=4k��AH=3k��

��Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5��3k��2��
�����ã�k2��3k��20.79=0��
���k=6.3��3.3����������
��OQ=5k=31.5��������������
��ʱx��ֵΪ��31.5��
��������������������x��ֵΪ��16.5��31.5��31.5��

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�