题目内容
函数y=ax+b的图象过点(0,1),(1,0),则0≤ax+b<1的解集是
0<x≤1
0<x≤1
.分析:先由函数y=ax+b的图象过点(0,1),(1,0),根据一次函数的性质得出当x=0时,y=1;当x=1时,y=0,且y随x的增大而减小,再根据一次函数与一元一次不等式的关系,得出0≤y<1时,0<x≤1,进而求出0≤ax+b<1的解集.
解答:解:∵函数y=ax+b的图象过点(0,1),(1,0),
∴当x=0时,y=1;当x=1时,y=0,
∴y随x的增大而减小,
∴0≤y<1时,0<x≤1,
即0≤ax+b<1的解集是0<x≤1.
故答案为0<x≤1.
∴当x=0时,y=1;当x=1时,y=0,
∴y随x的增大而减小,
∴0≤y<1时,0<x≤1,
即0≤ax+b<1的解集是0<x≤1.
故答案为0<x≤1.
点评:本题考查了一次函数的图象性质及一次函数与一元一次不等式的关系,难度适中,直线y=kx+b在x轴上方部分所有的点的横坐标所构成的集合即为不等式kx+b>0的解集.

练习册系列答案
相关题目
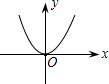
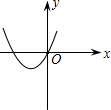
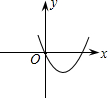
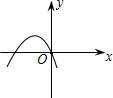
 13、函数y=ax+b的图象如图所示,则y随x的增大而
13、函数y=ax+b的图象如图所示,则y随x的增大而