题目内容
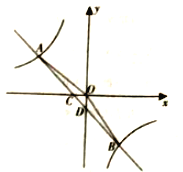
【题目】已知直线y=kx+b经过点A（﹣3，﹣8），且与直线
的公共点B的横坐标为6．
（1）求直线y=kx+b的表达式；
（2）设直线y=kx+b与y轴的公共点为点C，求△BOC的面积．
【答案】（1）
（2）12．
【解析】（1）先由已知直线求得点B的坐标，再根据待定系数法求得直线y=kx+b的表达式；
（2）先根据求得的直线解析式，求得点C的坐标，再根据点C和点B的位置，计算△BOC的面积．
解：（1）在直线
中，由 x=6，得
，
∴点B（6，4），
由直线y=kx+b经过点A、B，得
，解得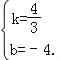 
∴所求直线表达式为
；
（2）在直线中，当 x=0时，得 y=﹣4，
即C（0，﹣4），
由点B（6，4）、C（0，﹣4），可得
△BOC的面积=
×4×6=12，
∴△BOC的面积为12．
“点睛”本题主要考查了两直线相交或平行的问题，解决问题的关键是掌握待定系数法求一次函数解析式，解题时注意：求一次函数y=kx+b，则需要两组x，y的值．
练习册系列答案
相关题目
