��Ŀ����
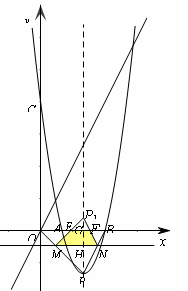
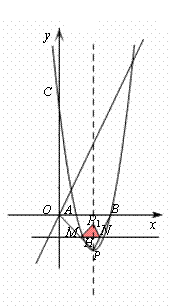
��֪���κ�����ͼ��A��2��0����C(0��12) ���㣬�ҶԳ���Ϊֱ��x=4. �趥��Ϊ
��P����x�����һ����Ϊ��B.
��1������κ����Ľ���ʽ������P�����ꣻ
��2����ͼ1����ֱ�� y=2x���Ƿ���ڵ�D��ʹ�ı���OPBDΪ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2����M���߶�OP�ϵ�һ�����㣨O��P������⣩����ÿ��![]() ����λ���ȵ��ٶ��ɵ�P���O �˶�������M��ֱ��MN��x�ᣬ��PB�ڵ�N. ����PMN��ֱ��MN���ۣ��õ���P1MN. �ڶ���M���˶������У����P1MN������OMNB���ص����ֵ����ΪS���˶�ʱ��Ϊt��. ��S����t�ĺ�����ϵʽ.
����λ���ȵ��ٶ��ɵ�P���O �˶�������M��ֱ��MN��x�ᣬ��PB�ڵ�N. ����PMN��ֱ��MN���ۣ��õ���P1MN. �ڶ���M���˶������У����P1MN������OMNB���ص����ֵ����ΪS���˶�ʱ��Ϊt��. ��S����t�ĺ�����ϵʽ.

�⣺��1������κ����Ľ���ʽΪy=ax2+bx+c
�������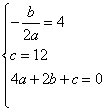 ���
���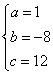
����κ����Ľ���ʽΪy= x2��8x+12
��P��������4����4��
��2�����ڵ�D��ʹ�ı���OPBDΪ��������. �������£�
��y=0ʱ��x2-8x+12=0 ��x1=2 �� x2=6
���B��������6��0��
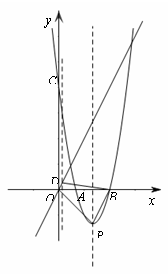 ��ֱ��BP�Ľ���ʽΪy=kx+m
��ֱ��BP�Ľ���ʽΪy=kx+m
��![]() ���
���![]()
��ֱ��BP�Ľ���ʽΪy=2x��12
��ֱ��OD��BP
�߶�������P��4�� ��4�� �� OP=4![]()
��D(x��2x) ��BD2=��2x��2+(6��x)2
��BD=OPʱ����2x��2+(6��x)2=32
��ã�x1=![]() ��x 2=2
��x 2=2
��x2=2ʱ��OD=BP=![]() ���ı���OPBDΪƽ���ı��Σ���ȥ
���ı���OPBDΪƽ���ı��Σ���ȥ
 �൱x=
�൱x=![]() ʱ�ı���OPBDΪ��������
ʱ�ı���OPBDΪ��������
�൱D(![]() ��
��![]() )ʱ���ı���OPBDΪ��������
)ʱ���ı���OPBDΪ��������
��3���� ��0��t��2ʱ��
���˶��ٶ�Ϊÿ��![]() ����λ���ȣ��˶�ʱ��Ϊt�룬
����λ���ȣ��˶�ʱ��Ϊt�룬
��MP=![]() t ��PH=t��MH=t��HN=
t ��PH=t��MH=t��HN=![]() t ��MN=
t ��MN=![]() t
t
��S=![]() t��t��
t��t��![]() =
=![]() t2
t2
�� ��2��t��4ʱ��P1G=2t��4��P1H=t
��MN��OB �� ![]() ��
��![]()
��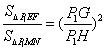 ��
�� 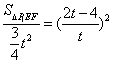
![]()
�� ![]() =3t2��12t+12
=3t2��12t+12
��S=![]() t2��(3t2��12t+12)= ��
t2��(3t2��12t+12)= ��![]() t2+12t��12
t2+12t��12
�� ��0��t��2ʱ��S=![]() t2
t2
��2��t��4ʱ��S=��![]() t2+12t��12
t2+12t��12