题目内容
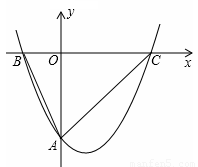
如图,经过原点的抛物线 与
与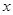 轴的另一个交点为A.过点
轴的另一个交点为A.过点 作直线
作直线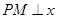 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
【小题1】当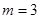 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
【小题2】当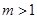 时,连结CA,问
时,连结CA,问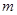 为何值时
为何值时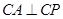 ?
?
【小题3】过点P作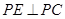 且
且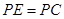 ,问是否存在
,问是否存在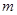 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的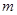 的值,并定出相对应的点E坐标;若不存在,请说明理由。
的值,并定出相对应的点E坐标;若不存在,请说明理由。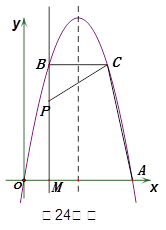
【小题1】当m=3时,y=-x²+6x
令y=0,得-x²+6x=0,
∴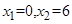 ∴A(6,0)
∴A(6,0)
当x=1时,y=5,∴B(1,5)
又∵抛物线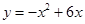 的对称轴为直线x=3,
的对称轴为直线x=3,
又∵B、C关于对称轴对称,∴BC="4" (4分)
【小题2】过点C作CH⊥x轴于点H(如图1)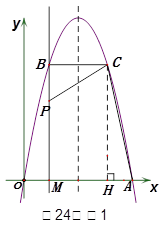
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB
又∵∠AHC=∠PBC=90°,
∴△ACH∽△PCB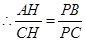
∵抛物线 的
的
对称轴为直线x=m,其中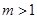 ,
,
又∵B,C关于对称轴对称,
∴BC=2(m-1)
∵B(1,2 m-1),P(1,m),
∴BP= m-1,
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0)
∴AH=1,CH=2m-1
∴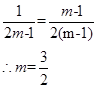 (8分)
(8分)
【小题3】∵B,C不重合,∴m≠1,
(Ⅰ)当m>1时,BC=2(m-1)
PM="m," BP= m-1.
(ⅰ)若点E在x轴上(如图2),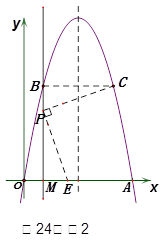
∵∠CPE=90°,
∴∠MPE+∠BPC=∠MPE+∠MEP =90°
∴∠MEP=∠BPC
又∵∠PME=∠CBP=90°,PC=EP
∴△BPC≌△MEP
∴BC=PM,
∴2(m-1)=m
∴m=2
此时点E的坐标是(2,0)
(ⅱ)若点E在y轴上(如图3)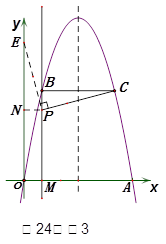
过点P作PN⊥y轴于点N,
易证△BPC≌△NPE,
∴BP=NP=OM=1,
∴ m-1=1,
∴m=2,
此时点E的坐标是(0,4)
(Ⅱ)当0<m<1时, BC=2(m-1),PM=m
BP= m-1.
(ⅰ) 若点E在x轴上(如图4),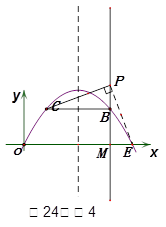
易证△PBC≌△MEP,
∴BC=PM
2(m-1)=m
∴m=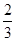
此时点E的坐标是(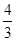 ,0)
,0)
(ⅱ)若点E在y轴上(如图5)
过点P作PN⊥y轴于点N,
易证△BPC≌△NPE,
∴BP=NP=OM=1,
∴ 1-m =1,
∴m=0,(∵m>0,舍去)
综上所述,当m=2时,点E的坐标是(2,0)或(0,4);
当m=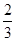 时,点E的坐标是(
时,点E的坐标是(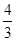 ,0)(14分)
,0)(14分)
解析

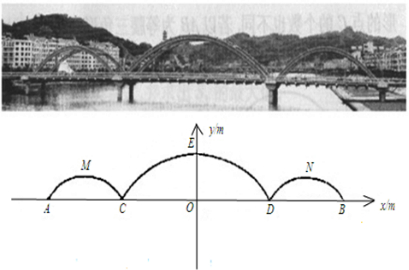
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为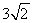
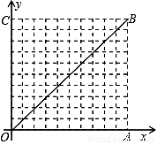
 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )