题目内容
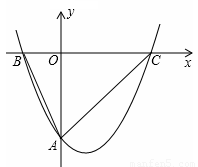
如图,经过点A(0,-4)的抛物线y=x2+bx+c与x轴相交于点B(-0,0)和C,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y=x2+bx+c向上平移个单位长度、再向左平移m(m>0)个单位长度,得到新抛物
线.若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.
解:(1)将A(0,-4)、B(-2,0)代入抛物线y=x2+bx+c中,得:
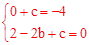 ,解得,
,解得, 。
。
∴抛物线的解析式:y=x2-x-4。源:ZXXK]
(2)由题意,新抛物线的解析式可表示为: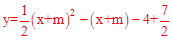 ,
,
即: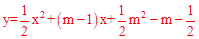 。它的顶点坐标P(1-m,-1)。
。它的顶点坐标P(1-m,-1)。
由(1)的抛物线解析式可得:C(4,0)。
∴直线AB:y=-2x-4;直线AC:y=x-4。
当点P在直线AB上时,-2(1-m)-4=-1,解得:m=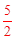 ;
;
当点P在直线AC上时,(1-m)+4=-1,解得:m=-2;
又∵m>0,
∴当点P在△ABC内时,0<m<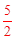 。
。
(3)由A(0,-4)、B(4,0)得:OA=OC=4,且△OAC是等腰直角三角形。
如图,在OA上取ON=OB=2,则∠ONB=∠ACB=45°。
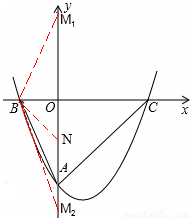
∴∠ONB=∠NBA+OAB=∠ACB=∠OMB+∠OAB,
即∠ONB=∠OMB。
如图,在△ABN、△AM1B中,
∠BAN=∠M1AB,∠ABN=∠AM1B,
∴△ABN∽△AM1B,得:AB2=AN•AM1;
由勾股定理,得AB2=(-2)2+42=20,
又AN=OA-ON=4-2=2,
∴AM1=20÷2=10,OM1=AM1-OA=10-4=6。
而∠BM1A=∠BM2A=∠ABN,∴OM1=OM2=6,AM2=OM2-OA=6-4=2。
综上,AM的长为6或2。
【解析】二次函数综合题,曲线上点的坐标与方程的关系,平移的性质,二次函数的性质,等腰直角三角形的判定和性质,勾股定理。
【分析】(1)该抛物线的解析式中只有两个待定系数,只需将A、B两点坐标代入即可得解。
(2)首先根据平移条件表示出移动后的函数解析式,从而用m表示出该函数的顶点坐标,将其
代入直线AB、AC的解析式中,即可确定P在△ABC内时m的取值范围。
(3)先在OA上取点N,使得∠ONB=∠ACB,那么只需令∠NBA=∠OMB即可,显然在y轴的正负半轴上都有一个符合条件的M点;以y轴正半轴上的点M为例,先证△ABN、△AMB相似,然后通过相关比例线段求出AM的长。

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案


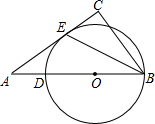 (2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.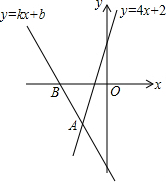 (2013•南通)如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为
(2013•南通)如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为 0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=
0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=