题目内容
【题目】阅读运用:
当方程中的系数用字母表示时,这样的方程叫做含字母系数的方程,也叫含参数的方程.
例如:2x+m=4,那么如何解这样的方程呢?实际上,我们可以把m当作常数,解出方程,
解得:2x=4﹣m.
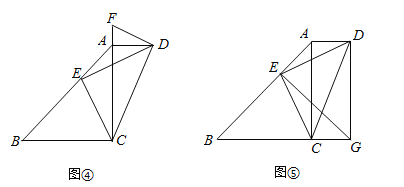
x= ![]() ,
,
请仿照上面的解法解答下列问题:
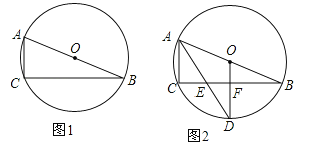
(1)解关于x,y的二元一次方程组 ![]() ,
,
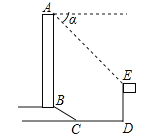
(2)若关于x,y的二元一次方程组: ![]() 的解满足不等式组
的解满足不等式组 ![]() ,求出整数a的所有值.
,求出整数a的所有值.
【答案】
(1)解: ![]() ,
,
①×2﹣②,得:3x=6a,
解得:x=2a,
将x=2a代入①,得:10a+2y=5a,
解得:y=﹣ ![]() a,
a,
∴方程组的解为 
(2)解:将  代入不等式组
代入不等式组 ![]() ,
,
得:  ,
,
解得:﹣2<a< ![]() ,
,
∴整数a的所有值为﹣1、0、1、2、3
【解析】(1)把a当作常数,利用加减消元法①×2﹣②可求出;(2)解出第一个方程组的解代入不等式组得出双边不等式,找出整数解.
【考点精析】通过灵活运用解一元一次方程的步骤和二元一次方程组的解,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目