题目内容
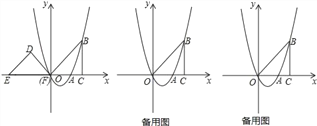
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() (
(![]() 且
且![]() )与
)与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作直线
作直线![]() 轴,且与
轴,且与![]() 交于点
交于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)若![]() ,
,![]() ,且
,且![]() 轴,判断四边形
轴,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)BC=1;(2)四边形OBDA是平行四边形,见解析.
【解析】
(1)理由待定系数法求出点D坐标即可解决问题;
(2)四边形OBDA是平行四边形.想办法证明BD=OA=3即可解决问题.
解:(1)当m=-2,n=1时,直线的解析式为y=-2x+1,
当x=1时,y=-1,
∴B(1,-1),
∴BC=1.
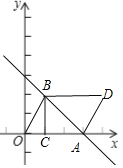
(2)结论:四边形OBDA是平行四边形.
理由:如图,∵BD∥x轴,B(1,1-m),D(4,3+m),
∴1-m=3+m,
∴m=-1,
∵B(1,m+n),
∴m+n=1-m,
∴n=3,
∴直线y=-x+3,
∴A(3,0),
∴OA=3,BD=3,
∴OA=BD,OA∥BD,
∴四边形OBDA是平行四边形.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】为了解某校七年级男生的身高(单位:![]() )情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
)情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
组别 |
|
|
|
|
|
身高 |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)样本容量是多少?组距是多少?组数是多少?
(2)画出适当的统计图表示上面的信息;
(3)若全校七年级学生有![]() 人,请估计身高不低于
人,请估计身高不低于![]() 的学生人数.
的学生人数.