题目内容
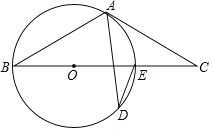
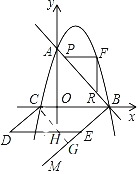
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与y轴交于点A,与x轴交于点B(3,0)、C(﹣1,0)两点.
(1)求直线AB和抛物线的表达式;
(2)当点F为直线AB上方抛物线上一动点(不与A、B重合),过点F作FP//x轴交直线AB于点P;过点F作FR//y轴交直线AB于点R,求PR的最大值;
(3)把射线BA绕着点B逆时针旋转90°得到射线BM,点E在射线BM运动(不与点B重合),以BC、BE为邻边作平行四边形BCDE,点H为DE边上动点,连接CH,请直接写出CH+![]() HE的最小值.
HE的最小值.

【答案】(1)抛物线的解析式为y=﹣x2+2x+3,直线AB的解析式为y=﹣x+3;(2)PR有最大值为![]() ;(3)最小值为2
;(3)最小值为2![]() .
.
【解析】
(1)将点B,C坐标代入抛物线解析式中,即可求出a,c,进而求出点A的坐标,再用待定系数法求出直线AB的解析式;
(2)先判断出∠OBA=∠OAB=45°,进而判断出∠FPR=∠FRP=45°,得出∠PFR=90°,PF=FR,进而得出PR=![]() FR,再设点R(t,﹣t+3),得出点F(t,﹣t2+2t+3),进而得出PR=
FR,再设点R(t,﹣t+3),得出点F(t,﹣t2+2t+3),进而得出PR=![]() FR=﹣
FR=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,即可得出结论;
,即可得出结论;
(3)过点C作CG⊥BM于G,交DE于点H,先判断出∠DEG=∠CBE=45°,进而判断出HG=![]() HE,根据垂线段最短和锐角三角函数即可得出结论.
HE,根据垂线段最短和锐角三角函数即可得出结论.
解:(1)∵抛物线y=ax2+2x+c经过点B(3,0)、C(﹣1,0),
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
令x=0,则y=3,
∴A(0,3),
∴设直线AB的解析式为y=kx+b(k≠0),
∵直线AB经过点A(0,3)、B(3,0),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=﹣x+3;
(2)∵A(0,3),B(3,0),
∴OA=OB=3,
∵∠AOB=90°,
∴∠OBA=∠OAB=45°,
∵FP//x轴,FR//y轴,
∴∠FPR=∠OBA=45°,∠FRP=∠OAB=45°,
∴∠FPR=∠FRP=45°,
∴∠PFR=90°,PF=FR,
根据勾股定理得,PR=![]() FR,
FR,
∵点R在直线AB上,
∴设点R(t,﹣t+3),
∵FR//y轴,
∴点F的横坐标为t,
∵点F在抛物线y=﹣x2+2x+3上,
∴点F(t,﹣t2+2t+3),
∴PR=![]() FR=
FR=![]() [(﹣t2+2t+3)﹣(﹣t+3)]=﹣
[(﹣t2+2t+3)﹣(﹣t+3)]=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,抛物线的开口向下,二次函数有最大值,
<0,抛物线的开口向下,二次函数有最大值,
当t=![]() 时,PR有最大值,PR的最大值为
时,PR有最大值,PR的最大值为![]() ;
;
(3)如图,过点C作CG⊥BM于G,交DE于点H,
∵把射线BA绕着点B逆时针旋转90°得到射线BM,
∴∠ABM=90°,
∵∠OBA=45°,
∴∠CBE=∠ABM﹣∠OBA=45°,
∵DE//CB,
∴∠DEG=∠CBE=45°,
在Rt△HGE中,HG=HEsin45°=![]() HE,
HE,
根据垂线段最短得,(CH+![]() HE)最小=CG,
HE)最小=CG,
∴CH+![]() HE=CG=CBsin45°=2
HE=CG=CBsin45°=2![]() ,
,
即CH+![]() HE的最小值为2
HE的最小值为2![]() .
.

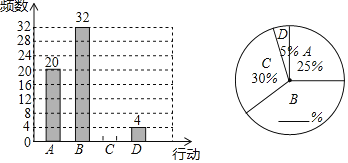
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.