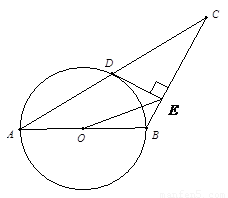题目内容
推理证明:如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D过D作DE⊥BC,垂足为E,连结OE,CD=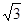 ,∠ACB=30°.
,∠ACB=30°.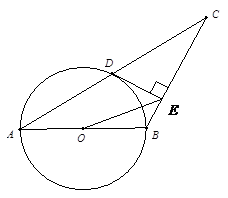
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
(1)见解析(2)2, (3)
(3) 解析:
解析:
(1)证明:连接BD
∵AB是直径,
∴∠ADB=90°
又∵AB=BC,
∴AD=CD,
∴OD∥BC
∴OD⊥DE,
∴DE是⊙O的切线.(4分)
(2)解:在Rt△CBD中CD= ,∠ACB=30°,
,∠ACB=30°,
∴BC="CD8" cos30° = =2,
=2,
∴AB=2.
在Rt△CDE中,CD= ,∠ACB=30°,
,∠ACB=30°,
∴DE=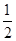 CD=
CD=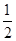 ×
× =
=  .
.
在Rt△ODE中,OE= =
= 
(3) ………9分
………9分
(1)根据AB是直径即可求得∠ADB,再根据题意可求出OD⊥DE,即得出结论;
(2)根据三角函数的定义,即可求得AB,再在Rt△CDE中,根据直角三角形的性质,可求得DE,再由勾股定理求出OE即可
(3)根据两圆的位置关系解答
 (3)
(3) 解析:
解析:(1)证明:连接BD

∵AB是直径,
∴∠ADB=90°
又∵AB=BC,
∴AD=CD,
∴OD∥BC
∴OD⊥DE,
∴DE是⊙O的切线.(4分)
(2)解:在Rt△CBD中CD=
 ,∠ACB=30°,
,∠ACB=30°,∴BC="CD8" cos30° =
 =2,
=2,∴AB=2.
在Rt△CDE中,CD=
 ,∠ACB=30°,
,∠ACB=30°,∴DE=
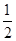 CD=
CD=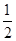 ×
× =
=  .
.在Rt△ODE中,OE=
 =
= 
(3)
 ………9分
………9分(1)根据AB是直径即可求得∠ADB,再根据题意可求出OD⊥DE,即得出结论;
(2)根据三角函数的定义,即可求得AB,再在Rt△CDE中,根据直角三角形的性质,可求得DE,再由勾股定理求出OE即可
(3)根据两圆的位置关系解答

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 完成下列推理过程:
完成下列推理过程: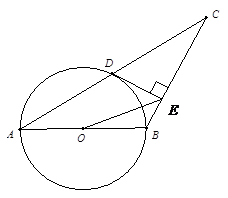
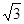 ,∠ACB=30°.
,∠ACB=30°.
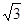 ,∠ACB=30°.
,∠ACB=30°.