Question

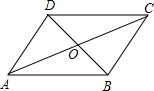如图，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=10、BD=8、AB=m，那么m的取值范围是（　　）

A．1＜m＜9

B．2＜m＜18

C．8＜m＜10

D．4＜m＜5

Answer 1

分析：由四边形ABCD是平行四边形，根据平行四边形的对角线互相平分，即可求得OA与OB的值，然后根据三角形三边关系，即可求得m的取值范围．

解答：解：∵四边形ABCD是平行四边形，
∴OA=OC=

1

2

AC=

1

2

×10=5，OB=OD=

1

2

BD=

1

2

×8=4，
∵OA-OB＜AB＜OA+OB，
∴5-4＜m＜5+4，
∴m的取值范围是：1＜m＜9．
故选A．

点评：此题考查了平行四边形的性质与三角形三边关系．此题难度不大，解题的关键是注意掌握平行四边形的对角线互相平分定理的应用，注意数形结合思想的应用．