题目内容
如图,在平面直角坐标系xOy中, 已知矩形ABCD的两个顶点B、C的坐标分别是B(1,0)、C(3,0).直线AC与y轴交于点G(0,6).动点P从点A出发,沿线段AB向点B运动.同时动点 Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC于点E.

(1)求直线AC的解析式;
(2)当t为何值时,△CQE的面积最大?最大值为多少?
(3)在动点P、Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使得以C、Q、E、H为顶点的四边形是菱形?

(1)求直线AC的解析式;
(2)当t为何值时,△CQE的面积最大?最大值为多少?
(3)在动点P、Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使得以C、Q、E、H为顶点的四边形是菱形?
(1)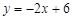 ;(2)2,1;(3)
;(2)2,1;(3)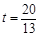 或
或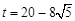
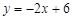 ;(2)2,1;(3)
;(2)2,1;(3)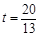 或
或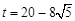
试题分析:(1)设直线AC的解析式为
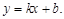 由图象经过G(0,6)、C(3,0)两点根据待定系数法求解即可;
由图象经过G(0,6)、C(3,0)两点根据待定系数法求解即可;(2)先求得点A的坐标,由AP=CQ=t,可得点P(1,4-t).将y=4–t代入
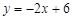 中,得点E的横坐标为x=
中,得点E的横坐标为x=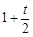 . 即得点E到CD的距离为
. 即得点E到CD的距离为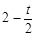 ,再根据三角形的面积公式及二次函数的性质求解即可;
,再根据三角形的面积公式及二次函数的性质求解即可;(3)过点E作FM∥DC,交AD于F,交BC于M.分当点H在点E的下方时,当点H在点E的上方时,根据菱形的性质及勾股定理求解即可.
(1)设直线AC的解析式为
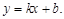
∵直线AC经过G(0,6)、C(3,0)两点,
∴
 解得
解得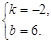
∴直线AC的解析式为
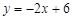 ;
;(2)在
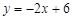 中,当x=1时,y="4." ∴A(1,4).
中,当x=1时,y="4." ∴A(1,4). ∵AP=CQ=t,
∴点P(1,4-t).
将y=4–t代入
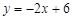 中,得点E的横坐标为x=
中,得点E的横坐标为x=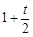 .
. ∴点E到CD的距离为
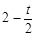 .
.∴S△CQE=
 =
=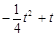 =
=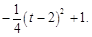
∴当t=2时,S△CQE最大,最大值为1;
(3)过点E作FM∥DC,交AD于F,交BC于M.
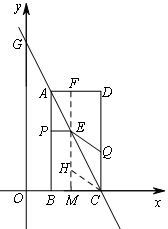
当点H在点E的下方时,连结CH.
∵
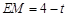 ,
,∴
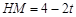 .
.∵
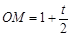 ,
,∴
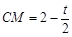 .
.∵四边形CQEH为菱形,
∴
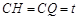 .
.在Rt△HMC中,由勾股定理得
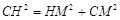 .
.∴
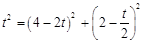 .
.整理得
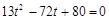 .
.解得
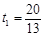 ,
,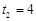 (舍).
(舍).∴当
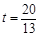 时,以C,Q,E,H为顶点的四边形是菱形.
时,以C,Q,E,H为顶点的四边形是菱形.当点H在点E的上方时,同理可得当
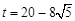 时. 以C,Q,E,H为顶点的四边形是菱形.
时. 以C,Q,E,H为顶点的四边形是菱形. ∴t的值是
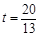 或
或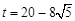 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为 

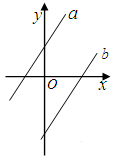
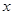 的一次函数
的一次函数 的图象正确的是 ( )
的图象正确的是 ( )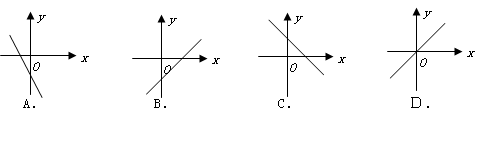
 由直线
由直线 :
: 沿
沿 轴向右平移9个单位得到,则直线
轴向右平移9个单位得到,则直线