题目内容
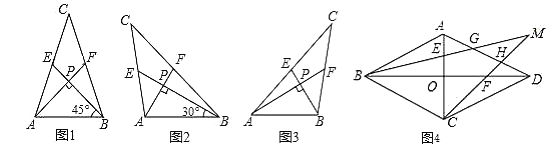
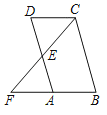
【题目】如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE;
(2)当E是AD的中点且BC=2CD时,直接写出图中所有与∠F相等的角.
【答案】(1)见解析;(2)图中所有与∠F相等的角为∠DCE、∠BCF、∠AEF、∠DCE,理由见解析
【解析】
(1)根据四边形ABCD是平行四边形就可以证明△CDE∽△FAE;
(2)根据(1)和E是AD的中点可以得到△CDE≌△FAE,然后根据全等三角形的性质和等腰三角形的性质即可得出答案.
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠DCE=∠F,∠CDE=∠FAE,
∴△CDE∽△FAE;
(2)解:图中所有与∠F相等的角为∠DCE、∠BCF、∠AEF、∠DCE,理由如下:
由(1)得:∠DCE=∠F,
∵△CDE∽△FAE,DE=EA,
∴△CDE≌△FAE,
∴CD=AF,
∴BF=2CD,
∵BC=2CD,AD=BC=2AE=2DE,
∴BF=BC,AF=AE,CD=DE,
∴∠F=∠BCF,∠AEF=∠F,∠DEC=∠DCE.

练习册系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.