题目内容
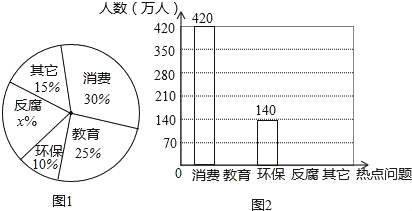
【题目】日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为![]() ,并把实验数据绘成两幅统计图(部分信息未给出):
,并把实验数据绘成两幅统计图(部分信息未给出):
![]()
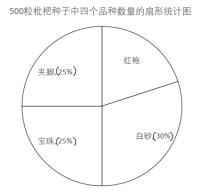
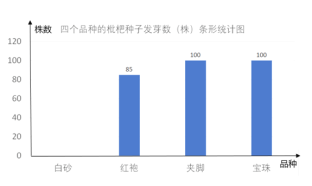
(1)求实验中“红袍”品种的种子数量;
(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
(3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.
【答案】(1)100;(2)图见解析;(3)应该选择“红袍”品种进行推广.
【解析】
(1)根据扇形图可知“红袍”品种的种子所占百分比,再用总数ד红袍”品种的种子所占百分比,求出“红袍”品种的种子数量.
(2)可用总数乘“白砂”品种的种子所占百分比,求出“白砂”品种的种子数量,从而补全统计图.
(3)根据条形统计图判断每个品种的种子发芽率,进而判断出推广的品种.
解:(1)“红袍”品种的种子数量:![]() (粒)
(粒)
(2)“白砂”品种的种子发芽的株数:![]() (株);
(株);
补全条形统计图如下:
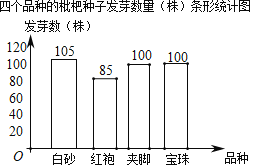 .
.
(3)“红袍”品种的种子发芽率:![]() ;
;
“宝珠”品种的种子发芽率:![]() ;
;
“夹脚”品种的种子发芽率:![]() ;
;
因此,应该选择“红袍”品种进行推广.

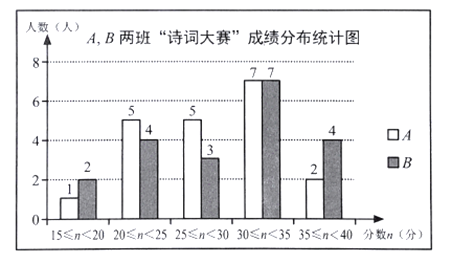
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③