题目内容
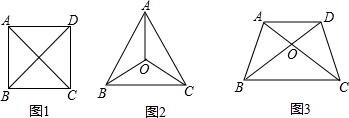
若等腰梯形ABCD的上、下底之和为2，并且两条对角线所成的锐角为60°，则等腰梯形ABCD的面积为 。
或
解析:分两种情况考虑：
（i）当∠AOB=∠COD=60°
∵四边形ABCD是等腰梯形
∴OA=OB，OC=OD
∵∠AOB=∠COD=60°
∴△OAB，△OCD均是等边三角形
设AB=x，则CD=2﹣x
∴OE=
x，OF=（2﹣x）
∴EF=
∴S梯形ABCD=
（AB+CD）•EF=×2×=；
（ii）当∠AOD=∠BOC=60°
∴∠AOB=∠COD=120°
∴∠OAB=∠OBA=∠ODC=∠OCD=30°
设AB=x，则CD=2﹣x
∴OE=
x，OF=
（2﹣x）
∴EF=
∴S梯形ABCD=
（AB+CD）•EF=×2×=
综上，等腰梯形ABCD的面积为
或．
练习册系列答案
名校课堂系列答案
相关题目
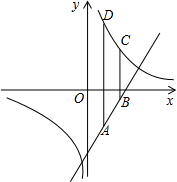当x=6时，反比例函数y=
