题目内容
25、在平面上有且只有4个点,这4个点中有一个独特的性质:连接每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.
(1)如图4,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.

(1)如图4,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.

分析:(1)①结合等腰梯形的性质及题意所表述的含义可写出符合题意的结论.②先证△ABC≌△DCB,得出∠DBC=∠ACB,根据题意可求得∠BDC=∠BCD=2∠ACB,设∠ACB=x°,利用内角和定理可得出答案.
(2)可选择画菱形.
(2)可选择画菱形.
解答:解:(1)①AB=DC=AD,AC=BD=BC,
②∵AC=BD,AB=DC,BC=BC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∵DC=AD,∠DAC=∠ACD,
∴∠ACD=∠ACB,
∵BC=BD,∠BDC=∠BCD=2∠ACB,
设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,
∴2x+2x+x=180,
解得x=36,
∴∠BCD=72°.
(2)所画图形如下:四边形ABCD是菱形,
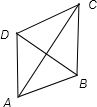
AB=BC=CD=AD=BD,AC.
②∵AC=BD,AB=DC,BC=BC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∵DC=AD,∠DAC=∠ACD,
∴∠ACD=∠ACB,
∵BC=BD,∠BDC=∠BCD=2∠ACB,
设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,
∴2x+2x+x=180,
解得x=36,
∴∠BCD=72°.
(2)所画图形如下:四边形ABCD是菱形,

AB=BC=CD=AD=BD,AC.
点评:本题考查等腰梯形的性质、三角形的内角和定理及全等三角形的判定,综合性较强,解答此类题目要注意仔细理解题目的意思,根据题意进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 (1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.