题目内容
(2013•河北一模)平面上有且只有4个点,这4个点中有一个独特的性质:连接每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC.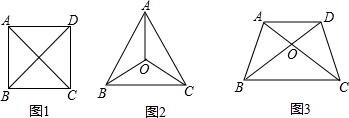
(1)如图3,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.写出相等的线段(不再添加字母);
(2)利用(1)的结论,求∠BCD的度数.

(1)如图3,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.写出相等的线段(不再添加字母);
(2)利用(1)的结论,求∠BCD的度数.
分析:(1)由等腰梯形ABCD的四个顶点是准等距点,且AD∥BC,即可求得答案;
(2)由(1)易证得△ABC≌△DCB,继而可得∠BDC=∠BCD=2∠ACB,然后设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,可得在△BDC中,2x+2x+x=180,继而可求得答案.
(2)由(1)易证得△ABC≌△DCB,继而可得∠BDC=∠BCD=2∠ACB,然后设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,可得在△BDC中,2x+2x+x=180,继而可求得答案.
解答:解:(1)∵等腰梯形ABCD的四个顶点是准等距点,且AD∥BC,
∴AB=DC=AD,AC=BD=BC;
(2)∵等腰梯形ABCD的四个顶点是准等距点,
∴AC=BD,AB=DC,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠DBC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∵DC=AD,
∴∠DAC=∠ACD,
∴∠ACD=∠ACB,
∵BC=BD,
∴∠BDC=∠BCD=2∠ACB,
设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,
∴在△BDC中,2x+2x+x=180,
解得x=36,
∴∠BCD=72°.
∴AB=DC=AD,AC=BD=BC;
(2)∵等腰梯形ABCD的四个顶点是准等距点,
∴AC=BD,AB=DC,
在△ABC和△DCB中,
|
∴△ABC≌△DCB(SSS),
∴∠DBC=∠ACB,
∵AD∥BC,
∴∠DAC=∠ACB,
∵DC=AD,
∴∠DAC=∠ACD,
∴∠ACD=∠ACB,
∵BC=BD,
∴∠BDC=∠BCD=2∠ACB,
设∠ACB=x°,则∠BDC=∠BCD=2x°,∠DBC=x°,
∴在△BDC中,2x+2x+x=180,
解得x=36,
∴∠BCD=72°.
点评:此题考查了的等腰梯形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
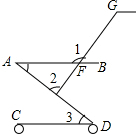 (2013•河北一模)如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
(2013•河北一模)如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )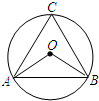 (2013•河北一模)如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为( )
(2013•河北一模)如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为( )