题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
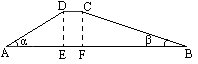
如图所示,作DE⊥AB,CF⊥AB,垂足分别为E,F.
在Rt△ADE中,因为sinα= |
(2) |
解:在Rt△ADE中,AE= 在Rt△ADE中,AE= 解题指导:作梯形的高构造直角三角形求解. |

练习册系列答案
相关题目

 如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线.
如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线. 已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4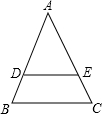 如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为