��Ŀ����
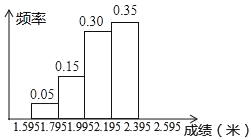
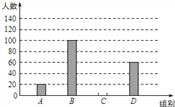
����Ŀ�����ҹ涨����Сѧ��ÿ����У�����ʱ�䲻����1Сʱ����Ϊ�ˣ�����������ÿ����У�����ʱ���Ƕ������������������������300������ѧ�������ݵ��������Ƴɵ�ͳ��ͼ�����֣���ͼ��ʾ�����з�������ǣ�
A�飺t��0.5h B�飺0.5h��t��1h C�飺1h��t��1.5h D�飺t��1.5h
�����������Ϣ����������⣺
��1��C����������� ����
��2�����ε������ݵ���λ�������� �����ڣ�
��3����������5400������ѧ��������������д���ҹ涨�����ʱ�����Լ�ж��٣�
���𰸡���1��120����2��C����3��3240��
�����������������
��1���ɱ����ѧ������Ϊ300�������ͳ��ͼ�е���֪���ݼ������C���������
��2������λ���Ķ����֪����300�����ݵ���λ���ǣ�����С�����˳�����к�ĵ�150�͵�151�����ݵ�ƽ���������ɣ�1���������ͳ��ͼ�е����ݿ�֪�����������ݶ���C�飬�ʿɵ��������ݵ���λ������C�飻
��3���ɣ�1��������C��������������ͳ��ͼ��D��������ɼ�����ﵽ���ҹ涨�������ʱ���������ռ�İٷֱȣ���5400��������ٷֱȼ��ɵõ������������.
���������
��1��C���������300����20+100+60��=120���ˣ���
�ʴ�Ϊ��120��
��2��������λ���ĸ����λ��Ӧ�ǵ�150��151��ʱ���ƽ�����������ɵ������C�飬
�ʵ������ݵ���λ������C�飬
�ʴ�Ϊ��C.
��3������ҹ涨�����ʱ�������Լռ![]() ��100%=60%��
��100%=60%��
�����ҹ涨�����ʱ�����Լ��5400��60%=3240���ˣ���

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ������=���멁�ɱ�������ָ���ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�