题目内容
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
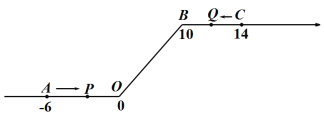
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
【答案】(1)15;4(2)t的值为2、3.5或5.
【解析】
(1)根据路程除以速度等于时,可得答案;根据相遇时P,Q的时间相等,可得方程,解出即可.
(2)根据PO与BQ的时间相等,可得方程,解出即可.
(1)点P运动至点C时,所需时间t=6÷2+10÷1+4÷2=15(s),
答:动点P从点A运动至C点需要15秒;
由题可知,P、Q两点相遇在线段OB上于M处,设OM=x.
则6÷2+x÷1=4÷1+(10-x)÷2,
x=4,
答:M所对应的数为4.
(2)P点运动完时间:6÷2+10÷1+4÷2=15(s)
Q点运动完时间:4÷1+10÷2+6÷1=15(s)
P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等有以下可能:
①动点Q在CB上,动点P在AO上,
则:4-1t=6-2t,解得:t=2.
②动点Q在CB上,动点P在OB上,
则:4-1t=1×(t-3),解得:t=3.5.
③动点Q在BO上,动点P在OB上,
则:2(t-4)=1×(t-3),解得:t=5.
④动点Q在OA上,动点P在OB上,
则:1×(t-9)+10=1×(t-3),无解
④动点Q在OA上,动点P在BC上,
则:1×(t-9)+10=2×(t-13)+10,解得:t=17>15,
综上所述:t的值为2、3.5或5.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名 | 批发价 | 零售价 |
黄瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?