题目内容
如图,矩形OABC的边OC、OA分别与x轴、y轴重合,点B的坐标是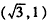 ,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折后,点A 落在点P处。
,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折后,点A 落在点P处。
(1)若点P在一次函数y=2x-l的图象上,求点P 的坐标;
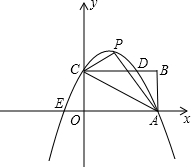
(2)若点P在抛物线y=ax2上,并满足△PCB是等腰三角形,求该抛物线解析式;
(3)当线段OD与PC所在直线垂直时,在PC所在直线上作出一点M,使DM+BM最小,并求出这个最小值。
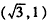 ,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折后,点A 落在点P处。
,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折后,点A 落在点P处。(1)若点P在一次函数y=2x-l的图象上,求点P 的坐标;
(2)若点P在抛物线y=ax2上,并满足△PCB是等腰三角形,求该抛物线解析式;
(3)当线段OD与PC所在直线垂直时,在PC所在直线上作出一点M,使DM+BM最小,并求出这个最小值。
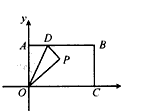
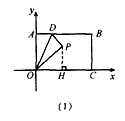
解:(1) ∵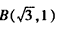 ∴BC=OA=OP=1, 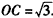 ∵点P在一次函数y=2x-1的图象上, ∴设P(x,2x-1), 如图(1),过P作PH⊥x轴于H, 在Rt△OPH中,PH=2x-1,OH=x,OP=1, ∴x2+(2x-1)2 =1, 解得x1=4/5,x2=0(不合题意,舍去) ∴P(4/5,3/5); |
 |
| (2)连接P、PC, ①若PB=PC,则P在BC中垂线y=1/2上, ∴设P(x,1/2), 如图(2),过P作PH⊥x轴于H, 在Rt△OPH中,PH=1/2,OH=x,OP=1, ∴x2+ 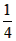 =1 =1解得 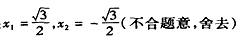 ∴ 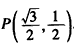 ∴1/2=a× 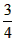 , ,解得a=2/3, ∴y= 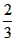 x; x;②若BP=BC,则BP=1, 连接OB, ∵OP=1, ∴OP+PB=2, ∵在Rt△OBC中,∠OCB=90°,OB= 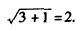 ∴OP+PB=OB, ∴O、P、B三点共线,P为OB中点, 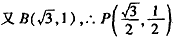 ∴1/2=a× 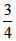 , ,解得:a=2/3, ∴y= 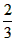 x2 x2③若CP=CB,则CP=1, ∴PO=PC,则P在OC中垂线 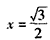 上, 上,∴设 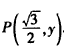 ,过P作PH⊥x轴于H, ,过P作PH⊥x轴于H,在Rt△OPH中, 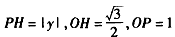 ∴y2+ 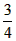 =1, =1,解得:y1=1/2,y2=-1/2 时, ∴ 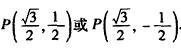 当点 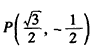 时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意, 时,∠AOP=120°,此时∠AOD=60°,点D与点B重合,符合题意,若 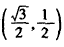 点,则1/2=a× 点,则1/2=a×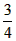 , ,解得:a=2/3, ∴y= 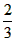 x2 x2若 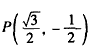 点,则-1/2=a× 点,则-1/2=a×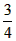 , ,解得:a=-2/3, ∴y=- 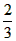 x2 x2 |
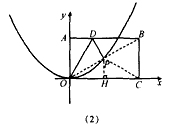 |
| (3)如图(3),∵△OAD沿OD翻折,点A落在点P处, ∴OD垂直平分AP, ∵PC⊥OD, ∴A、P、C三点共线, 在Rt△AOD中,∠OAD=90°,OA=1, 又可得:∠AOD=30°, ∴AD=AO · tan30°= 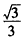 , ,∴  作点B关于直线AC的对称点B′,过点B′作B′N⊥AB于点N,连接DB′,DB′与AC交点为M,此点为所求点, ∵∠ACB′- ∠ACB=60°,∠ACO=30°, ∴∠B′CO=30°, ∵B′C=BC=1, ∴ 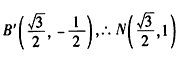 在Rt△B′ND中, ∠B′ND=90°,B′N=3/2,DN=AN-AD = 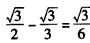 ∴  ∴DM+ BM的最小值为 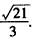 。 。 |
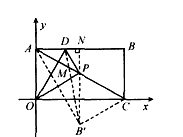 (3) |

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是