题目内容
【题目】(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E,当直线MN旋转到图1的位置时,求证:DE=AD+BE;
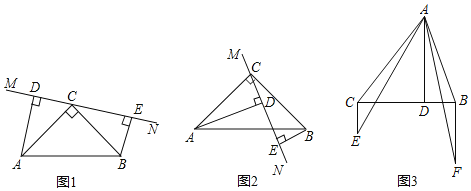
(2)在(1)的条件下,当直线MN旋转到图2的位置时,猜想线段AD,DE,BE的数量关系,并证明你的猜想;
(3)如图3,在△ABC中,AD⊥BC于D,AD=BC,BF⊥BC于B,BF=CD,CE⊥BC于C,CE=BD,求证:∠EAF+∠BAC=90°.
【答案】(1)见解析;(2)DE=AD﹣BE,证明见解析;(3)见解析.
【解析】
(1)由已知条件可推出∠ACD=∠CBE,继而可证明△ADC≌△CEB,利用全等三角形的性质可证明结论;
(2)与(1)证法类似,可推出∠ACD=∠CBE,证明△ADC≌△CEB,得出AD=CE,DC=BE,继而得出结论;
(3)连接CF、BE,可证明△ADC≌△CBF,进一步推出△ACF为等腰直角三角形,同理可推出△ABE为等腰直角三角形,从而可得出结论.
解:(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)DE=AD﹣BE,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)如图3,连接CF、BE,
AD⊥BC于D,BF⊥BC于B,
∴∠ADC=∠CBF=90°,
在△ADC和△CBF中,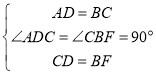 ,
,
∵△ADC≌△CBF(SAS),
∴∠CAD=∠FCB,AC=CF;
∴∠ACF=∠FCB+∠ACD=∠CAD+∠ACD=∠ADC=90°
∴△ACF为等腰直角三角形.
∴∠CAF=45°,
同理:△ABE为等腰直角三角形.
∴∠EAB=45°,
∴∠EAF+∠BAC=∠CAF+∠EAB=90°.

 53随堂测系列答案
53随堂测系列答案【题目】我市启动了第二届“美丽港城美在阅读”全民阅读活动.为了解市民每天的阅读时间情况,随机抽取了部分市民进行调查.根据调查结果绘制如下尚不完整的频数分布表:
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
(1) 补全表格;
(2) 将每天阅读时间不低于 ![]() 的市民称为“阅读爱好者”.若我市约有
的市民称为“阅读爱好者”.若我市约有 ![]() 万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?