题目内容
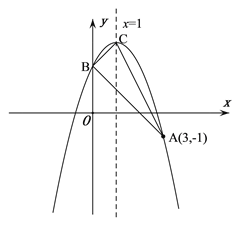
【题目】如图,直线y=﹣![]() x+n交x轴于点A,交y轴于点C(0,4),抛物线y=
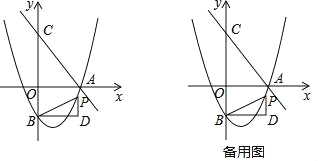
x+n交x轴于点A,交y轴于点C(0,4),抛物线y=![]() x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
(1)求抛物线的解析式;
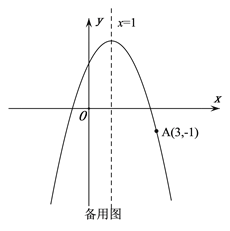
(2)当△BDP为等腰直角三角形时,求线段PD的长.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)PD=
x﹣2;(2)PD=![]() .
.
【解析】
(1)由点C坐标,得直线方程为:y=-![]() x+n=-
x+n=-![]() x+4,从而求出点A坐标,把点A、B坐标代入二次函数表达式即可求解;
x+4,从而求出点A坐标,把点A、B坐标代入二次函数表达式即可求解;
(2)设点P(m,![]() m2-
m2-![]() m-2),当△BDP为等腰直角三角形时,BD=PD,即可求解.
m-2),当△BDP为等腰直角三角形时,BD=PD,即可求解.
(1)由点C坐标,得直线方程为:y=﹣![]() x+n=﹣
x+n=﹣![]() x+4,
x+4,
令y=0,解得:x=3,则点A(3,0),
把点A、B坐标代入二次函数表达式,
解得:b=﹣![]() ,c=﹣2,
,c=﹣2,
则函数表达式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)设点P(m,![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
点B(0,﹣2),则点D(m,﹣2),
当△BDP为等腰直角三角形时,BD=PD,
即:![]() m2﹣
m2﹣![]() m﹣2﹣(﹣2)=m,
m﹣2﹣(﹣2)=m,
解得:m=![]() ,(m=0舍去),
,(m=0舍去),
PD=BD=m=![]() .
.

练习册系列答案
相关题目