题目内容
如图：P是正方形ABCD内一点，将△ABP绕点B顺时针旋转能与△CBP′重合，若PB=5，求PP′的长．
分析：利用正方形的性质和旋转的性质，求出∠ABP=∠CBP′，BP=BP′，∠PBP′=90°；利用直角三角形的性质求出PP′=5
．
| 2 |
解答：解：∵ABCD为正方形，
∴∠ABC=90°．
∵△ABP顺时针旋转后能与△CBP′重合，
∴∠ABP=∠CBP′，BP=BP′，
∴∠PBP′=90°，
∴Rt△PBP′中，BP=BP′=5，
∴PP′=5
．
∴∠ABC=90°．
∵△ABP顺时针旋转后能与△CBP′重合，
∴∠ABP=∠CBP′，BP=BP′，
∴∠PBP′=90°，
∴Rt△PBP′中，BP=BP′=5，
∴PP′=5
| 2 |
点评：本题考查旋转的性质和正方形的性质，旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
如图，E是正方形ABCD对角线AC上一点，EF⊥AB，EG⊥BC，F、G是垂足，若正方形ABCD周长为a，则EF+EG等于（ ）A、
| ||
B、
| ||
| C、a | ||
| D、2a |
22、如图，ABCD是正方形，P是对角线BD上一点，过P点作直线EF、GH分别平行于AB、BC，交两组对边于E、F、G、H，则四边形PEDG，四边形PHBF都是正方形，四边形PEAH、四边形PGCF都是矩形，设正方形PEDG的边长是a，正方形PHBF的边长是b． 请动手实践并得出结论：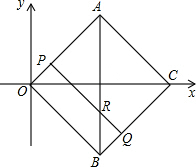
，两点运动到相遇停止．设△OPQ的面积为S．请求出S关于t的函数关系式以及自变量t的取值范围．
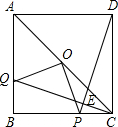点P，连接OP，OQ；