题目内容
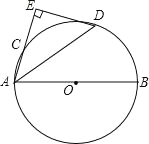
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行可得AE与OD平行,由两直线平行同旁内角互补,得到∠E与∠EDO互补,再由∠E为直角,可得∠EDO为直角,即DE为圆O的切线,得证;
(2)连接BD,过点A作AF⊥AC,由AB为圆O的直径,根据直径所对的圆周角为直角,得到∠ADB为直角,在直角三角形ABD中,利用锐角三角函数定义得到cos∠DAB的值,又在直角三角形AED中,由AE及AD的长,利用锐角三角函数定义求出cos∠EAD的值,由∠EAD=∠DAB,得到cos∠EAD=cos∠DAB,得出cos∠DAB的值,即可求出直径AB的长,由勾股定理和垂径定理即可求出AC长.
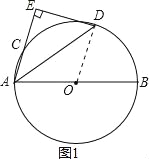
试题解析:(1)连接OD,如图1所示:
∵AD为∠CAB的平分线,
∴∠CAD=∠BAD,
又∵OA=OD,
∴∠BAD=ODA,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠E+∠EDO=180°,
又∵AE⊥ED,即∠E=90°,
∴∠EDO=90°,
则ED为圆O的切线;
(2)连接BD,如图2所示,过点A作AF⊥AC,
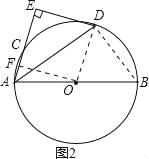
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△ABD中,cos∠DAB=![]() ,
,
在Rt△AED中,AE=4,AD=5,
∴cos∠EAD=![]() ,又∠EAD=∠DAB,
,又∠EAD=∠DAB,
∴cos∠DAB=cos∠EAD=![]() ,
,
则AB=![]() AD=
AD=![]() ,即圆的直径为
,即圆的直径为![]() ,
,
∴AO=![]() ,
,
∵∠E=∠EDO=∠EFO=90°,
∴四边形EFOD是矩形,
∴OF=DE=3,
∴AF=![]() ,
,
∴AC=2AF=![]() .
.

 计算高手系列答案
计算高手系列答案