题目内容
如图，已知∠ACB=70°，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=________．
17.5°
分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
解答：设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，
∴4x=70°，
∴x=17.5°，
即∠E=17.5°．
故答案为：17.5°．
点评：本题主要考查了等边对等角的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并列出方程是解题的关键．
分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
解答：设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，
∴4x=70°，
∴x=17.5°，
即∠E=17.5°．
故答案为：17.5°．
点评：本题主要考查了等边对等角的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并列出方程是解题的关键．
练习册系列答案
相关题目
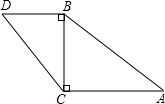如图，已知∠ACB=∠CBD=90°，BC=a，AC=b，当CD=（ ）时，△CDB∽△ABC．A、
| ||||
B、
| ||||
C、
| ||||
D、
|
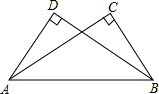如图，已知∠ACB=∠BDA=90°，要使△ABC≌△BAD，还需要添加一个条件，这个条件可以是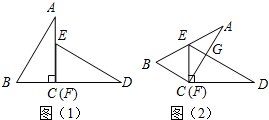
如图，已知∠ACB=90°，∠DAB=70°，AC平分∠DAB，∠1=35°．