题目内容
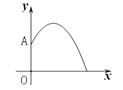
【题目】某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是![]() ,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4
【答案】D
【解析】分析:在已知抛物线解析式的情况下,利用其性质,求顶点(最大高度),与x轴,y轴的交点,解答题目的问题.
详解:当x=0时,y=3,故柱子OA的高度为3m;(1)正确;
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点是(1,4),
故喷出的水流距柱子1m处达到最大高度,喷出的水流距水平面的最大高度是4米;故(2)(3)正确;
解方程-x2+2x+3=0,
得x1=-1,x2=3,
故水池的半径至少要3米,才能使喷出的水流不至于落在水池外,(4)正确.
故选:C.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目