题目内容
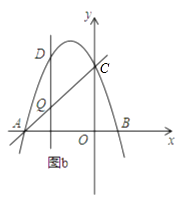
【题目】已知一抛物线与x轴的交点是A(﹣2,0)、B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
【答案】
(1)解:设这个抛物线的解析式为y=ax2+bx+c;
由已知,抛物线过A(﹣2,0),B(1,0),C(2,8)三点,得  ;
;
解这个方程组,得a=2,b=2,c=﹣4;
∴所求抛物线的解析式为y=2x2+2x﹣4
(2)解:y=2x2+2x﹣4=2(x2+x﹣2)=2(x+ ![]() )2﹣
)2﹣ ![]() ,
,
∴该抛物线的顶点坐标为(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】此题考查了待定系数法求a、b、c的值,根据题意可得三元一次方程组,解方程组即可求得待定系数的值;利用配方法或公式法求顶点坐标即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
相关题目