题目内容
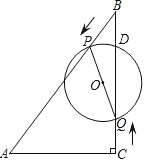
【题目】如图,在 Rt△ABC 中,∠ACB=90°,AC=6cm,∠ABC=30°,动点 P 从点 B 出发,在 BA 边上以每秒 2cm 的速度向点 A 匀速运动,同时动点 Q 从点 C 出发,在 CB 边上以每秒![]() cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
(1)当 t=1 时,求△BPQ 的面积;
(2)设⊙O 的面积为 y,求 y 与 t 的函数解析式;
(3)若⊙O 与 Rt△ABC 的一条边相切,求 t 的值.
【答案】(1)![]() ;(2)y=
;(2)y=![]() t2-18πt+27π;(3)t 的值为 3 或
t2-18πt+27π;(3)t 的值为 3 或![]() 或 0 或
或 0 或![]() .
.
【解析】
(1)连接DP,根据△BPM~△BAC,可得PD=t,BQ=![]() (6-t),然后得到
(6-t),然后得到
![]() =
=![]() BQ·PD即可得出结论;
BQ·PD即可得出结论;
(2)先表示出DP,BD,进而利用勾股定理求出PQ的平方,最后用圆的面积公式即可得出结论;
(3)分![]() O与BC相切、
O与BC相切、![]() O与AB相切,
O与AB相切, ![]() O与AC相切时,三种情况分类讨论即可得出结论.
O与AC相切时,三种情况分类讨论即可得出结论.
解:
(1)如图 1,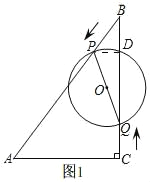
在 Rt△ABC 中,∠ABC=30°,AC=6,
∴AB=12,BC=6![]() ,
,
由运动知,BP=2t,CQ=![]() t,
t,
∴BQ=BC﹣CQ=![]() (6﹣t),连接 DP,
(6﹣t),连接 DP,
∵PQ 是⊙O 的直径,
∴∠PDQ=90°
∵∠C=90°,
∴PD∥AC.
∴△BPD∽△BAC,
∴![]() =
=![]()
∴![]() =
=![]() ,
,
∴DP=t,BD= ![]() t,
t,
![]() =
= ![]() BQPD=
BQPD= ![]() ×(6﹣t)t=﹣
×(6﹣t)t=﹣![]() t
t![]() +3
+3![]() t
t
∴当 t=1 时,![]() =
=![]() ﹣
﹣![]() +3
+3![]() =
=![]() ;
;
(2)DQ=|BQ﹣BD|=| ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() t|=2
t|=2![]() |3﹣t|,PQ
|3﹣t|,PQ![]() =PD
=PD![]() +DQ
+DQ![]() =t
=t![]() +[2
+[2![]()
(3﹣t)]![]() =13t
=13t![]() ﹣72t+108,
﹣72t+108,
∴y=π×(![]() )
)![]() =
= ![]() t
t![]() ﹣18πt+27π,
﹣18πt+27π,
(3)由运动知,BP=2t,CQ=![]() t,
t,
∴BQ=BC﹣CQ=![]() (6﹣t),当⊙O 与 BC 相切时,PQ⊥BC,
(6﹣t),当⊙O 与 BC 相切时,PQ⊥BC,
∴△BPQ∽△BAC,
∴![]()
∴![]()
∴![]() =3,
=3,
当⊙O 与 AB 相切时,PQ⊥AB,
∴△BPQ∽△BCA
∴![]()
∴![]()
∴![]() =
= ![]() ,
,
当⊙O 与 AC 相切时,
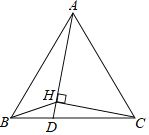
如图 2 ,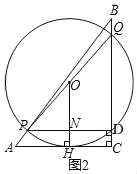
过点 O 作 OH⊥AC 于点 H,交 PD 于点 N,
∴OH∥BC,
∵点 O 是 PQ 的中点,
∴ON= ![]() QD,
QD,
由(1)知,BQ=![]() (6﹣t),BD=
(6﹣t),BD=![]() t,
t,
∴QD=BD﹣BQ=2![]() (t﹣3),DC=BC﹣BD=6
(t﹣3),DC=BC﹣BD=6![]() ﹣
﹣![]() t=
t=![]() (6﹣t)
(6﹣t)
∴OH=ON+NH= ![]() QD+DC=
QD+DC= ![]() ×2 (t﹣3)+ (6﹣t)=3 ,
×2 (t﹣3)+ (6﹣t)=3 ,
∴PQ=2OH=6![]() ,
,
由(2)知,PQ![]() =13t
=13t![]() ﹣72t+108
﹣72t+108
∴13t![]() ﹣72t+108=36×3解得
﹣72t+108=36×3解得 ![]() =0,
=0,![]() =
=![]() ,
,
综上所述,若⊙O 与 Rt△ABC 的一条边相切,t 的值为 3 或![]() 或 0 或
或 0 或![]() .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
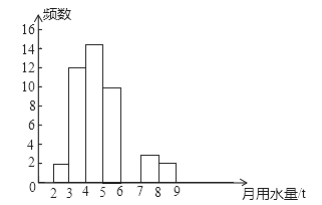
三点一测快乐周计划系列答案【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.