题目内容
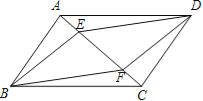
【题目】已知:如图,在ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形.
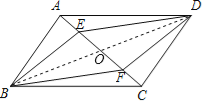
【答案】证明:连续BD交AC于点O
∵ 四边形ABCD是平行四边形
∴ AO = CD,DO = BO
∵ AE = CF
∴ AO – AE =" CO" – CF,即EO = FO
∴ 四边形EBFD是平等四边形
【解析】试题分析:先连接BD,交AC于O,由于四边形ABCD是平行四边形,易知OB=OD,OA=OC,而AE=CF,根据等式性质易得OE=OF,再根据两组对角线互相平分的四边形是平行四边形可证之.
试题解析:连接BD,交AC于O, ∵四边形ABCD是平行四边形, ∴OB=OD,OA=OC, ∵AE=CF,
∴OA﹣AE=OC﹣CF, ∴OE=OF, ∴四边形BFDE是平行四边形.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x | ﹣1 | 0 | 0.5 | 2 |
y | ﹣1 | 2 | 3.75 | 2 |
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=2是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<2时,ax2+(b﹣1)x+c>0.
上述结论中正确的有( )个.
A.1 B.2 C.3 D.4