Question

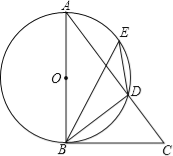
【题目】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A、C的坐标分别为A（﹣3，0），C（1，0），．

（1）求过点A、B的直线的函数表达式；

（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；

（3）在（2）的条件下，如P、Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得以点A、P、Q为顶点的三角形与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．

Answer 1

【答案】（1）直线AB的解析式为y=x+；（2）符合条件的D（，0）；（3）符合要求的m的值为 或.

【解析】

(1)根据点A、B的坐标求出AC的长度再根据求出BC的长度 然后即可写出点B的坐标，设过点A,B的直线的函数表达式为y＝ kx＋b，利用待定系数法求解即可得到直线AB的函数表达式；

(2)过点B作BD⊥AB,交x轴于点D,D点为所求，继而求出D点坐标；

(3)在Rt△ABC中，由勾股定理得AB的值，当PQ// BD时，△APQ~△ABD ,解得m的值 ;当PQ⊥AD时，△APQ ~△ADB ,则解得m 的值.

（1）∵A（﹣3，0），C（1，0），

∴AC=4，

∵BC=AC，

∴BC=×4=3，

∴B（1，3），

设直线AB的解析式为y=kx+b，

∴，

∴，

∴直线AB的解析式为y=x+；

（2）若△ADB与△ABC相似，

过点B作BD⊥AB交x轴于D，∴∠ABD=∠ACB=90°，如图1，

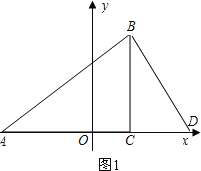
此时 =，即AB2=ACAD．

∵∠ACB=90°，AC=4，BC=3，

∴AB=5，

∴25=4AD，

∴AD=，

∴OD=AD﹣AO=﹣3=，

∴点D的坐标为（ ，0）．

即：符合条件的D（ ，0）．

（3）∵AP=DQ=m，

∴AQ=AD﹣QD=﹣m．

Ⅰ、若△APQ∽△ABD，如图2，

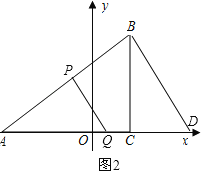
则有 =，

∴APAD=ABAQ，

∴m=5（ ﹣m），

解得m=；

Ⅱ、若△APQ∽△ADB，如图3，

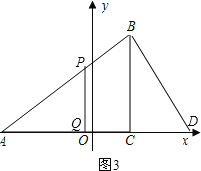
则有 =，

∴APAB=ADAQ，

∴5m=（ ﹣m），

解得：m=，

综上所述：符合要求的m的值为 或 ．