题目内容
对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
①<1.493>=1;
②<2x>=2<x>;
③若 ,则实数x的取值范围是
,则实数x的取值范围是 ;
;
④当x≥0,m为非负整数时,有 ;
;
⑤ 。
。
其中,正确的结论有 (填写所有正确的序号)。
 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:①<1.493>=1;
②<2x>=2<x>;
③若
 ,则实数x的取值范围是
,则实数x的取值范围是 ;
;④当x≥0,m为非负整数时,有
 ;
;⑤
 。
。其中,正确的结论有 (填写所有正确的序号)。
①③④。
①根据定义,∵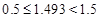 ,∴<1.493>=1。结论正确。
,∴<1.493>=1。结论正确。
②用特例反证:∵<1.3>=1,<2×1.3>=<2.6>=3,∴<2×1.3>≠2<1.3>。
∴<2x>=2<x>不一定成立。结论错误。
③若 ,则
,则 。
。
∴实数x的取值范围是 。结论正确。
。结论正确。
④设2013x=k+b,k为2013x的整数部分,b为其小数部分,
1)当0≤b<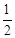 时,<2013x>=k,
时,<2013x>=k,
m+2013x=(m+k)+b,m+k为m+2013x的整数部分,b为其小数部分,< m+2013x>=m+k,
∴< m+2013x >=m+<2013x>。
2)当b≥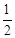 时,<2013x>=k+1,
时,<2013x>=k+1,
则m+2013x=(m+k)+b,m+k为m+2013x的整数部分,b为其小数部分,< m+2013x >=m+k+1,
∴< m+2013x >=m+<2013x>
综上:当x≥0,m为非负整数时,< m+2013x >=m+<2013x>成立。结论正确。
⑤用特例反证::<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>。∴ 不一定成立。结论错误。
不一定成立。结论错误。
综上所述,正确的结论有①③④。
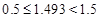 ,∴<1.493>=1。结论正确。
,∴<1.493>=1。结论正确。②用特例反证:∵<1.3>=1,<2×1.3>=<2.6>=3,∴<2×1.3>≠2<1.3>。
∴<2x>=2<x>不一定成立。结论错误。
③若
 ,则
,则 。
。∴实数x的取值范围是
 。结论正确。
。结论正确。④设2013x=k+b,k为2013x的整数部分,b为其小数部分,
1)当0≤b<
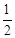 时,<2013x>=k,
时,<2013x>=k,m+2013x=(m+k)+b,m+k为m+2013x的整数部分,b为其小数部分,< m+2013x>=m+k,
∴< m+2013x >=m+<2013x>。
2)当b≥
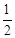 时,<2013x>=k+1,
时,<2013x>=k+1,则m+2013x=(m+k)+b,m+k为m+2013x的整数部分,b为其小数部分,< m+2013x >=m+k+1,
∴< m+2013x >=m+<2013x>
综上:当x≥0,m为非负整数时,< m+2013x >=m+<2013x>成立。结论正确。
⑤用特例反证::<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>。∴
 不一定成立。结论错误。
不一定成立。结论错误。综上所述,正确的结论有①③④。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,并求出它的自然数解.
,并求出它的自然数解. ,并把解集在数轴上表示.
,并把解集在数轴上表示.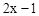 的值在1(含1)与3(含3)之间;
的值在1(含1)与3(含3)之间; 的解集为
的解集为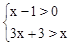 的解集是 .
的解集是 .