题目内容
如图,△ 是等边三角形,点
是等边三角形,点 坐标为(-8,0)、点
坐标为(-8,0)、点 坐标为(8,0),点
坐标为(8,0),点 在
在 轴的正半轴上.一条动直线从
轴的正半轴上.一条动直线从 轴出发,以每秒1个单位长度的速度沿
轴出发,以每秒1个单位长度的速度沿 轴向右平移,直线与直线
轴向右平移,直线与直线 交于点
交于点 ,与线段
,与线段 交于点
交于点 .以
.以 为边向左侧作等边△
为边向左侧作等边△ ,
, 与
与 轴的交点为
轴的交点为 .当点
.当点 与点
与点 重合时,直线停止运动,设直线的运动时间为(秒).
重合时,直线停止运动,设直线的运动时间为(秒).

(1)填空:点 的坐标为 ,四边形
的坐标为 ,四边形 的形状一定是 ;
的形状一定是 ;
(2)试探究:四边形 能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
(3)当t为何值时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上?并求出此时⊙
上?并求出此时⊙ 的半径.
的半径.
 是等边三角形,点
是等边三角形,点 坐标为(-8,0)、点
坐标为(-8,0)、点 坐标为(8,0),点
坐标为(8,0),点 在
在 轴的正半轴上.一条动直线从
轴的正半轴上.一条动直线从 轴出发,以每秒1个单位长度的速度沿
轴出发,以每秒1个单位长度的速度沿 轴向右平移,直线与直线
轴向右平移,直线与直线 交于点
交于点 ,与线段
,与线段 交于点
交于点 .以
.以 为边向左侧作等边△
为边向左侧作等边△ ,
, 与
与 轴的交点为
轴的交点为 .当点
.当点 与点
与点 重合时,直线停止运动,设直线的运动时间为(秒).
重合时,直线停止运动,设直线的运动时间为(秒).
(1)填空:点
 的坐标为 ,四边形
的坐标为 ,四边形 的形状一定是 ;
的形状一定是 ;(2)试探究:四边形
 能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
能不能是菱形?若能,求出相应的的值;若不能,请说明理由.(3)当t为何值时,点
 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上?并求出此时⊙
上?并求出此时⊙ 的半径.
的半径.(1)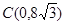 ,四边形
,四边形 是平行四边形(2)当
是平行四边形(2)当 秒时,四边形
秒时,四边形 为菱形(3)当
为菱形(3)当 秒时,点
秒时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,此时⊙
上,此时⊙ 的半径为
的半径为
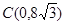 ,四边形
,四边形 是平行四边形(2)当
是平行四边形(2)当 秒时,四边形
秒时,四边形 为菱形(3)当
为菱形(3)当 秒时,点
秒时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,此时⊙
上,此时⊙ 的半径为
的半径为
解:(1)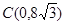 ,四边形
,四边形 是平行四边形
是平行四边形
…………(3分)
(2)由 及
及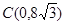 可求得直线
可求得直线 的解析式为
的解析式为
 …………(4分)
…………(4分)
∴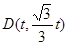 ,
, ,
,
则 …………(5分)
…………(5分)
由(1)知,四边形 是平行四边形
是平行四边形
∴要使四边形 为菱形,则必须有
为菱形,则必须有 成立;设与
成立;设与 轴交于点
轴交于点 ,
,
∵
∴ …………(7分)
…………(7分)
解得
∴当 秒时,四边形
秒时,四边形 为菱形…………(8分)
为菱形…………(8分)
(3)如图2,连结 ,
,

当 时,点
时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,…………(9分)
上,…………(9分)
此时,点 为
为 的中点
的中点
∴
由(1)知,四边形 是平行四边形
是平行四边形
∴ …………(10分)
…………(10分)
又由(2)知, ,
,
∴
解得 …………(12分)
…………(12分)
∴当 秒时,点
秒时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,此时⊙
上,此时⊙ 的半径为
的半径为 …………(13分)
…………(13分)
注:第(3)小题的解法有多种,请自行制定相应的评分标准.
(1)由勾股定理求出OC,得到C的坐标,动直线沿 轴向右平移,可知四边形
轴向右平移,可知四边形 的形状一定是平行四边形
的形状一定是平行四边形
(2)由 及
及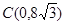 可求得直线
可求得直线 的解析式,通过D、E两点求得直线DE的解析式, 有
的解析式,通过D、E两点求得直线DE的解析式, 有 成立,求得相应的的值
成立,求得相应的的值
(3)连结 ,由(1)、(2)的结论求得
,由(1)、(2)的结论求得
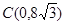 ,四边形
,四边形 是平行四边形
是平行四边形…………(3分)
(2)由
 及
及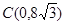 可求得直线
可求得直线 的解析式为
的解析式为 …………(4分)
…………(4分)∴
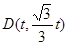 ,
, ,
,则
 …………(5分)
…………(5分)由(1)知,四边形
 是平行四边形
是平行四边形∴要使四边形
 为菱形,则必须有
为菱形,则必须有 成立;设与
成立;设与 轴交于点
轴交于点 ,
,∵

∴
 …………(7分)
…………(7分)解得

∴当
 秒时,四边形
秒时,四边形 为菱形…………(8分)
为菱形…………(8分)(3)如图2,连结
 ,
,
当
 时,点
时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,…………(9分)
上,…………(9分)此时,点
 为
为 的中点
的中点∴

由(1)知,四边形
 是平行四边形
是平行四边形∴
 …………(10分)
…………(10分)又由(2)知,
 ,
,
∴

解得
 …………(12分)
…………(12分)∴当
 秒时,点
秒时,点 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上,此时⊙
上,此时⊙ 的半径为
的半径为 …………(13分)
…………(13分)注:第(3)小题的解法有多种,请自行制定相应的评分标准.
(1)由勾股定理求出OC,得到C的坐标,动直线沿
 轴向右平移,可知四边形
轴向右平移,可知四边形 的形状一定是平行四边形
的形状一定是平行四边形(2)由
 及
及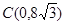 可求得直线
可求得直线 的解析式,通过D、E两点求得直线DE的解析式, 有
的解析式,通过D、E两点求得直线DE的解析式, 有 成立,求得相应的的值
成立,求得相应的的值(3)连结
 ,由(1)、(2)的结论求得
,由(1)、(2)的结论求得
练习册系列答案
相关题目
 和直线
和直线 交于点P, 则根据图象可得,关于
交于点P, 则根据图象可得,关于 、
、 的二元一次方程组
的二元一次方程组 的解是 .
的解是 .
 的图象不经过( ).
的图象不经过( ). 与直线
与直线 的图象交x轴于同一点,则
的图象交x轴于同一点,则 之间的关系式为_________。
之间的关系式为_________。 (
( >0,)上一定点,点A是
>0,)上一定点,点A是 轴上一动点(不与原点重合),连结PA,过点P作PB⊥PA,交
轴上一动点(不与原点重合),连结PA,过点P作PB⊥PA,交 轴于点B,探究线段PA与PB 的数量关系.
轴于点B,探究线段PA与PB 的数量关系.


