题目内容
已知正六边形的边心距为
，则它的周长是（ ）
| 3 |
| A、6 | ||
| B、12 | ||
C、6
| ||
D、12
|
分析：设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得边长AB，从而求出周长．
解答：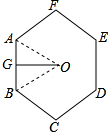
解：如图，在Rt△AOG中，OG=
，∠AOG=30°，
∴cos30°=
，
∴OA=OG÷cos 30°=2．
这个正六边形的周长=12．
故选B．
解：如图，在Rt△AOG中，OG=| 3 |
∴cos30°=
| OG |
| AO |
∴OA=OG÷cos 30°=2．
这个正六边形的周长=12．
故选B．
点评：此题主要考查正多边形的计算问题，属于常规题．解题的关键是正确的构造直角三角形．
练习册系列答案
相关题目
已知正六边形的边心距为
，则正六边形的边长为（ ）
| 3 |
A、2
| ||
| B、2 | ||
| C、1 | ||
D、
|