题目内容
已知正六边形的边心距r6为3厘米,则它的半径长=
2
| 3 |
2
厘米,面积=| 3 |
18
| 3 |
18
平方厘米.| 3 |
分析:根据正六边形的性质连接DO,EO,得出∠DON=30°,进而利用锐角三角函数关系得出DO,进而得出△EOD的面积即可得出正六边形面积.
解答: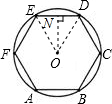 解:如图所示:连接DO,EO,过点O作ON⊥DE垂足为N,
解:如图所示:连接DO,EO,过点O作ON⊥DE垂足为N,
由题意可得出:∠DON=30°,
∵正六边形的边心距r6为3厘米,
∴cos∠DON=
=
,
则DO=
=2
(cm),
∴DE=DO=EO=2
cm,
∴S△EOD=
×NO×DE=
×2
×3=3
(cm2),
∴正六边形面积为:3
×6=18
(cm2).
故答案为:2
,18
.
 解:如图所示:连接DO,EO,过点O作ON⊥DE垂足为N,
解:如图所示:连接DO,EO,过点O作ON⊥DE垂足为N,由题意可得出:∠DON=30°,
∵正六边形的边心距r6为3厘米,
∴cos∠DON=
| NO |
| DO |
| 3 |
| DO |
则DO=
| 3 |
| cos30° |
| 3 |
∴DE=DO=EO=2
| 3 |
∴S△EOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴正六边形面积为:3
| 3 |
| 3 |
故答案为:2
| 3 |
| 3 |
点评:此题主要考查了正多边形和圆的性质,根据已知得出∠DON的度数是解题关键.

练习册系列答案
相关题目
已知正六边形的边心距为
,则正六边形的边长为( )
| 3 |
A、2
| ||
| B、2 | ||
| C、1 | ||
D、
|
已知正六边形的边心距为
,则它的周长是( )
| 3 |
| A、6 | ||
| B、12 | ||
C、6
| ||
D、12
|