题目内容
已知：如图，四边形ABCD内接于以BC为直径的⊙O，且AB=AD，延长CB、DA，交于P点，CE与⊙O相切于点C，CE与PD的延长线交于点E．当PB=OC，CD=18时，求DE的长．
如图，连接OA、BD，OA与BD交于F点，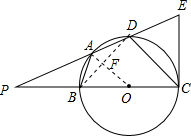
∵AB=AD，
∴弧AB=弧AD，
∴OA⊥BD，BF=DF，
而OB=OC，
∴OF=
DC=9，
∵BC为⊙O的直径，
∴∠BDC=90°，
∴OA∥DC，
∴△PAO∽△PDC，
∴
=
=
，
∵PB=OC，CD=18，
∴
=
=
，解得OA=12，PA=
PD，即PD=3AD，
∴AF=12-9=3，
在Rt△OAF中，BF=
=3
，
在Rt△ABF中，AB=
=6
，
∴PD=3×6
=18
，
∵CE与⊙O相切于点C，
∴CE⊥PC，EC2=DE•EA，
在Rt△PCE中，EC2=PE2-PC2，
∴DE•EA=PE2-PC2，即DE（DE+6
）=（18
+DE）2-362，
∴DE=
．
∵AB=AD，
∴弧AB=弧AD，
∴OA⊥BD，BF=DF，
而OB=OC，
∴OF=
| 1 |
| 2 |
∵BC为⊙O的直径，
∴∠BDC=90°，
∴OA∥DC，
∴△PAO∽△PDC，
∴
| PO |
| PC |
| OA |
| DC |
| PA |
| PD |
∵PB=OC，CD=18，
∴
| 2OB |
| 3OB |
| OA |
| 18 |
| PA |
| PD |
| 2 |
| 3 |
∴AF=12-9=3，
在Rt△OAF中，BF=
| 122-92 |
| 7 |
在Rt△ABF中，AB=
| BF2+AF2 |
| 2 |
∴PD=3×6
| 2 |
| 2 |
∵CE与⊙O相切于点C，
∴CE⊥PC，EC2=DE•EA，
在Rt△PCE中，EC2=PE2-PC2，
∴DE•EA=PE2-PC2，即DE（DE+6
| 2 |
| 2 |
∴DE=
54
| ||
| 5 |
练习册系列答案
相关题目
的延长线于C点．