题目内容
8、如果一个三角形的一条边上的中点到其他两边的距离相等，那么这个三角形一定是（ ）
分析：三角形的一条边上的中点到其他两边的距离相等，利用全等证明三角形全等，得到两角相等，从而证明两边相等，所以是等腰三角形．
解答：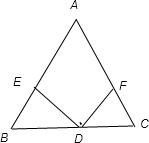
已知：△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，E、F为垂足，且DE=DF．
求三角形的形状．
解：连接AD，∵DE⊥AB，DF⊥AC，E、F为垂足，且DE=DF，
D是BC的中点，BD=CD，
∴Rt△BDE≌Rt△DFC，
∴∠B=∠C，
∴AB=AC．
一个三角形的一条边上的中点到其他两边的距离相等，那么这个三角形一定是等腰三角形．
故选A．
已知：△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，E、F为垂足，且DE=DF．求三角形的形状．
解：连接AD，∵DE⊥AB，DF⊥AC，E、F为垂足，且DE=DF，
D是BC的中点，BD=CD，
∴Rt△BDE≌Rt△DFC，
∴∠B=∠C，
∴AB=AC．
一个三角形的一条边上的中点到其他两边的距离相等，那么这个三角形一定是等腰三角形．
故选A．
点评：本题主要考查了角平分线的性质和全等的判定与性质；证明三角形全等是正确解答本题的关键．
练习册系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目