题目内容
如果一个三角形的一条边上的中点到其他两边的距离相等,那么它一定是( )
A.等边三角形 B.等腰三角形
C.不等边三角形 D.不等腰钝角三角形
【答案】
B
【解析】
试题分析:三角形的一条边上的中点到其他两边的距离相等,利用全等证明三角形全等,得到两角相等,从而证明两边相等,所以是等腰三角形.
已知:△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,E、F为垂足,且DE=DF,判断三角形的形状.
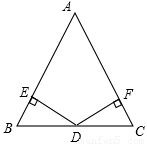
连接AD,∵DE⊥AB,DF⊥AC,E、F为垂足,且DE=DF,
D是BC的中点,BD=CD,
∴Rt△BDE≌Rt△DFC,
∴∠B=∠C,
∴AB=AC.
一个三角形的一条边上的中点到其他两边的距离相等,那么这个三角形一定是等腰三角形.
故选B.
考点:本题主要考查了角平分线的性质和全等的判定与性质
点评:证明三角形全等是正确解答本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目